Absolute Value
Absolute Value Functions
Transformations
In previous units, transformations of quadratics and other polynomials were discussed. The transformations so far follow these rules:
- f (x) + k is f(x) shifted upward k units
- f (x) - k is f(x) shifted downward k units
- f (x + h) is f(x) shifted left h units
- f (x - h) is f(x) shifted right h units
- -f(x) is f(x) flipped upside down ("reflected about the x-axis")
- f (-x) is the mirror of f(x) ("reflected about the y-axis")
- a• f(x) stretches the graph vertically if a > 1
- a•f(x) shrinks the graph vertically if 0 < a < 1
Transformations of absolute value functions follow these rules as well. For an absolute value, the function notation for the parent function is f(x) = IxI and the transformation is f(x) = a Ix - hI + k. For example, f(x) = 2 Ix - 2I +1 is graphed below along with the parent function:
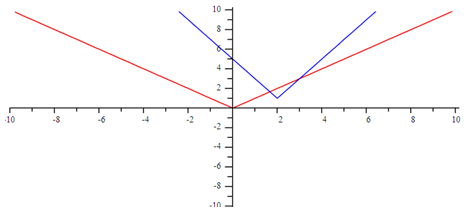
As you can see, the transformation is stretched vertically by 2, moved to the right 2 units, and up 1 unit from the parent function.