Absolute Value
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra I |
| Book: | Absolute Value |
| Printed by: | Guest user |
| Date: | Saturday, January 31, 2026, 4:10 PM |
Description
Absolute Value Functions
Introduction
The absolute value of x, denoted "|x|" and read "the absolute value of x", is the distance x is from zero on a number line. This is why absolute value is never negative; absolute value asks "how far?" not "in which direction?" For instance, 4 and -4 have the same absolute value of 4:So, the absolute value of a positive number is the number itself, and the absolute value of a negative number is its opposite. The absolute value of zero is 0.
The absolute value bars do not work in the same way as do parentheses. Where -(-3) = +3, this is not true in -|-3|. To simplify -|-3| first simplify the absolute value part. The distance -3 is from zero is 3 units so the absolute value of -3 is 3, so -|-3| = - (+3) = -3.
Solving Equations
When solving absolute value equations algebraically, the x needs to be isolated. However, because the x is inside the absolute value bars, there are additional steps needed. For example, what is the solution for IxI = 3? This is asking, what values are a distance of three units from zero. There are actually two solutions. X can be substituted by 3 because I3I =3, but x can also be substituted by -3 because I-3I is equal to 3. Both numbers are 3 units away from zero on the number line. Therefore, most absolute value equations will have two solutions.To solve, IxI + 2 = 10, use the following steps:
Step 1. Isolate the absolute value bars using inverse operations.
|x| + 2 - 2 = 10 - 2
|x| = 8
Step 2. Write two equations.
b. Write the other equation to equal the negative.
IxI = 8
x = 8 and x = -8
The solutions are 8 and -8.
Step 3. Check the solutions.
![]()
Example 1
Solve Ix - 4I + 1 = 9.Step 1. Isolate the absolute value bars using inverse operations.
Ix - 4I + 1 - 1 = 9 - 1
Ix - 4I = 8
Step 2. Write two equations.
b. Write the other equation to equal the negative.
x - 4 = 8 and x - 4 = -8
x - 4 + 4 = 8 + 4 and x - 4 + 4 = -8 + 4
x = 12 and x = -4
Step 3. Check the solutions.
Example 2
Solve 5 Ix - 2I = 30.Step 1. Isolate the absolute value bars using inverse operations.
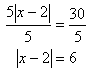
Step 2. Write two equations.
b. Write the other equation to equal the negative.
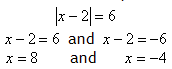
Video Lesson
For a video on solving absolute value equations, select the following link:Solving Absolute Value Equations
Interactive Practice
For interactive practice on solving absolute value equations, select the following link:Solving Absolute Value Equations
Practice
Solving Absolute Value WorksheetAnswer Key
Solving Absolute Value Answer KeyGraphing
A function of the form f(x) = a Ix - hI + k is an absolute value function. The graph of an absolute value equation is represented by the equation y = a Ix - hI + k. The graphs of absolute value equations in two variables are v-shaped. The vertex, which is the maximum or minimum point of the graph, is the point (h, k) found in the equation. The graph of the parent function y = |x| looks like this: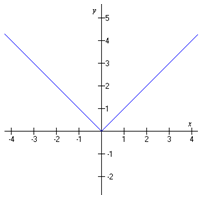
The vertex of the graph above is (0, 0). An absolute value function has some similarities to a quadratic. The functions can both be written in vertex form and their graphs are both symmetrical.
Example 1
Graph the equation y = Ix - 3I - 2.Step 1. Determine the vertex of the equation.
The (h, k) of the equation, (3, -2), will be the vertex of the graph.
Step 2. Determine the a-value of the equation.
Since the a-value of the equation is 1, the slope of the line to the right of the vertex is +1 and the slope of the line to the left of the vertex is -1.
Step 3. Make a graph of the equation.
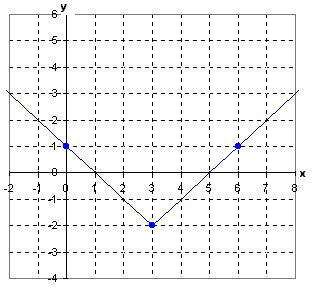
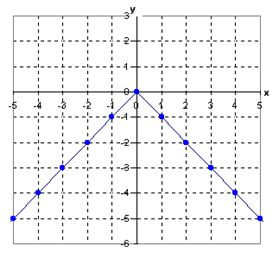
Example 2
Graph y = - IxI.Step 1. Determine the vertex of the equation.
The (h, k) of the equation, (0, 0), will be the vertex of the graph.
Step 2. Determine the a-value of the equation.
Since the a-value of the equation is -1, the slope of the line to the right of the vertex is -1 and the slope of the line to the left of the vertex is +1.
Step 3. Make a graph of the equation.
Transformations
In previous units, transformations of quadratics and other polynomials were discussed. The transformations so far follow these rules:
- f (x) + k is f(x) shifted upward k units
- f (x) - k is f(x) shifted downward k units
- f (x + h) is f(x) shifted left h units
- f (x - h) is f(x) shifted right h units
- -f(x) is f(x) flipped upside down ("reflected about the x-axis")
- f (-x) is the mirror of f(x) ("reflected about the y-axis")
- a• f(x) stretches the graph vertically if a > 1
- a•f(x) shrinks the graph vertically if 0 < a < 1
Transformations of absolute value functions follow these rules as well. For an absolute value, the function notation for the parent function is f(x) = IxI and the transformation is f(x) = a Ix - hI + k. For example, f(x) = 2 Ix - 2I +1 is graphed below along with the parent function:
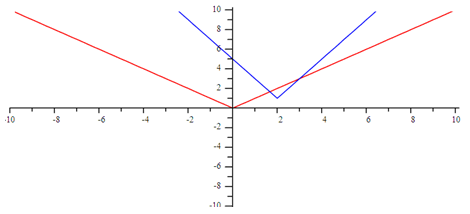
As you can see, the transformation is stretched vertically by 2, moved to the right 2 units, and up 1 unit from the parent function.
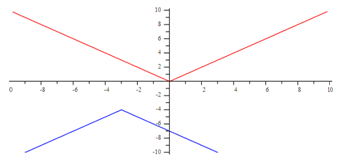
Example
Graph the function f(x) = - Ix + 3I - 4. Explain how this graph would compare to the parent function.Step 1. Explain the a-value.
Since a = -1, the graph is reflected across the x-axis.
Step 2. Explain the h-value.
Since h = -3, the graph will translate 3 units left.
Step 3. Explain the k-value.
Since k = -4, the graph will translate 4 units down.
Step 4. Make a graph.
Using Calculators to Graph
To learn more about using a TI 83/84 to graph and solve absolute value equations, please select the following link:Calculator instructions
Solving by Graphing
Absolute value equations can be solved by graphing as well as algebraically. Suppose the given equation is 3 Ix + 5I - 2 = 10. Graph the left side of the equation and the right side separately and calculate where the two graphs intersect. The intersection points of the two graphs are the solutions of the original equation.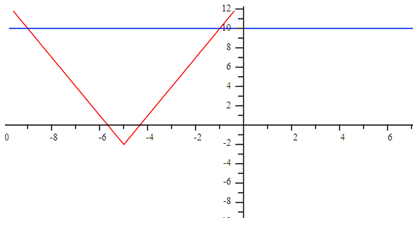
You can see by the graph that there are two solutions, where the red and blue graphs intersect. This is something absolute value functions also have in common with quadratics. In this case, the solutions are x = -1 and x = -9 which can be verified by solving algebraically.
Practice
Graphing Absolute Value WorksheetAnswer Key
Graphing Absolute Value Answer KeySources
Algebasics, http://www.algebasics.com/3way5.html (accessed 08/22/2010).
Coffman, Joseph. "Absolute Value Functions." http://www.jcoffman.com/Algebra2/ch2_5.htm (accessed 08/22/2010).
Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project
Holt, Rinehart, & Wilson, http://my.hrw.com/math06_07/nsmedia/ lesson_videos/alg2/player.html?contentSrc=7774/7774.xml (accessed 08/22/2010).
Hot Math, "Absolute Values." http://hotmath.com/hotmath_help/ topics/absolute-value.html (accessed 08/22/2010).
Hot Math, "Practice Problems." http://hotmath.com/help/gt/genericalg1 /section_4_3.html (accessed 08/22/2010).
MathBits.com, "Absolute Values." http://mathbits.com/MathBits/ TISection/Algebra2/absolutevalue.htm (accessed 08/22/2010).
Purple Math, "Absolute Value." http://www.purplemath.com/modules/ absolute.htm (accessed 08/22/2010).
Purple Math, "Function Transformations." http://www.purplemath.com/ modules/fcntrans2.htm (accessed 08/22/2010).