Graphing Overview
Graphing Families Overview
Logarithmic Functions
Prior to Algebra II, logarithmic functions have not been presented. An overview is presented here. This content will be fully developed in a later unit. When given an exponential function, such as
, it can be rewritten in logarithmic form as 
.
Logarithmic functions are in the form: 
; 
. The graph of a logarithmic function will turn from a steep increase to an extremely slow gradual rise.
See the table and graph of a basic logarithmic function below.
|
|
 |
|
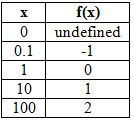
Here are some situations that can be modeled by logarithmic functions:
- Richter scale for earthquakes (magnitude vs. energy).
- Measurement of sound (decibels vs. intensity).
- Cram studying (amount forgotten vs. time).