Graphing Overview
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra II KHauck |
| Book: | Graphing Overview |
| Printed by: | Guest user |
| Date: | Friday, January 23, 2026, 12:01 PM |
Description
Graphing Families Overview
Introduction
Every family of functions has unique characteristics in terms of their symbolic, tabular, contextual, and graphical representations. After completing Algebra I and Algebra II, there should be a firm understanding of functions and function notation.
This unit will review families of functions learned in Algebra I and introduce new families of functions which will be presented in greater detail later in this course.
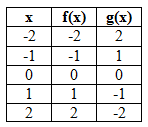
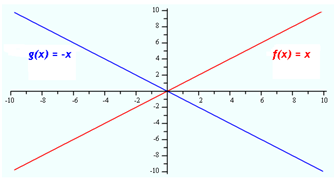
Linear Functions
The most familiar family of functions is linear. Linear functions include the constant functions and the functions that increase or decrease at a constant rate.Linear functions have equations in the form: f(x) = mx + b, where m is the constant rate of change or slope and b is the starting value or y-intercept.
See the table and graph of two basic linear functions below.
 |
 |
Here are some situations that model linear functions:
- An airplane flies at a constant altitude (height vs. time).
- A bathtub fills at a constant rate (volume vs. time).
- Weekly deposits of equal paychecks (amount vs. time).
Guided Practice
To solidify your understanding of linear functions, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials, and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.Linear Functions Guided Practice
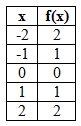
Absolute Value Functions
Absolute value is defined as a number’s distance from zero. Since distance is always positive or zero, absolute value functions will always produce positive or zero outputs.Absolute value functions have equations in the form:
See the table and graph of a basic absolute value function below.
 |

|
Here are some situations that can be modeled by absolute value functions:
- Distances in real life (time vs. distance).
- Exchanging currency (old currency vs. new).
Power Functions
A power function is a function where the variable has a power greater than one. Graphs of power functions will vary depending upon the value of the exponent.
Power functions have equations in the form: ![]() . There are patterns in the shapes of the graphs of power functions. Power functions take two forms:
. There are patterns in the shapes of the graphs of power functions. Power functions take two forms: ![]() and
and ![]() . All power functions with even powers will graph similar to
. All power functions with even powers will graph similar to ![]() and power functions with odd powers will graph similar to
and power functions with odd powers will graph similar to ![]() .
.
See the table and graph of two basic power functions below.
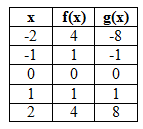 |
f(x) = x2 g(x) = x3
|
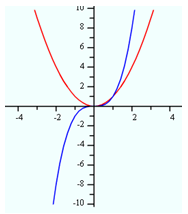
|
Here are some situations that can be modeled by power functions:
- Area (area vs. length).
- Volume (volume vs. length).
- A falling object (height vs. time).
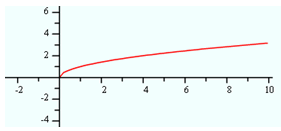
Square Root Functions
A square root function is a function that contains a variable under the square root symbolSquare root functions have equations in the form:
See the table and graph of a basic square root function below.
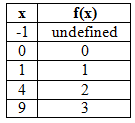 |
f(x) = ?x
|
Here are some situations that can be modeled by square root functions:
- Power factor and electrical load distribution (power vs. load).
- Collision detection for polygon shaped objects (direction vs. size).
- Fly ball behind the plate (distance vs. time).
Video Lesson
To learn more about square root functions select the following link:Square Root Functions
Guided Practice
To solidify your understanding of square root functions, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.Square Root Guided Practice
Exponential Functions
An exponential function is a function where a variable is found in the exponent. Exponential functions model many real life situations and are prevalent in news data.Exponential functions are in the form:
See the table and graph of a basic exponential function below.
![]()
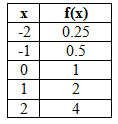 |
|
Here are some situations that can be modeled by exponential functions:
- Savings accumulating compound interest (amount vs. time).
- The spread of rumors (insiders vs. time).
- The decay of radioactive elements (amount vs. time).
Rational Functions
Prior to Algebra II, rational functions have not been presented. An overview is given here. This content will be fully developed in a later unit. Rational functions are the ratio of polynomials, in other words one polynomial divided by another.Rational functions are in the form:
See the table and graphs of two of the most basic rational functions below.

| |
|

|

|
Here are some situations that can be modeled by rational functions:
- A lighthouse beam moving along a shoreline (velocity vs. angle).
- Pressure of a compressed gas (pressure vs. distance).
- Repellant forces at close range (force vs. distance).
Logarithmic Functions
Prior to Algebra II, logarithmic functions have not been presented. An overview is presented here. This content will be fully developed in a later unit. When given an exponential function, such as![]() , it can be rewritten in logarithmic form as
, it can be rewritten in logarithmic form as ![]() .
.
Logarithmic functions are in the form: ![]() ;
; ![]() . The graph of a logarithmic function will turn from a steep increase to an extremely slow gradual rise.
. The graph of a logarithmic function will turn from a steep increase to an extremely slow gradual rise.
See the table and graph of a basic logarithmic function below.
![]()
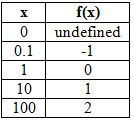

- Richter scale for earthquakes (magnitude vs. energy).
- Measurement of sound (decibels vs. intensity).
- Cram studying (amount forgotten vs. time).
Interactive Activity
This set of exercises allows you to practice making connections and distinctions among the various families of functions and their representations.
Practice
Identify the Family of Functions Worksheet*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,†refresh your browser.
Answer Key
Identify Family of Functions Answer Key
*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,†refresh your browser.
Sources
Sources used in this book:Embracing Mathematics, Assessment & Technology in High Schools; a Michigan Mathematics & Science Partnership Grant Project
Holt, Rinehart, & Winston, "Exponential and Radical Functions." http://my.hrw.com/math06_07/nsmedia/homework_help/alg1/alg1_ch11_05_homeworkhelp.html (accessed 06/30/2010).
Holt, Rinehart, & Winston, "Linear Functions." http://my.hrw.com/math06_07/nsmedia/homework_help/alg1/alg1_ch05_01_homeworkhelp.html (accessed 06/30/2010).
Mueller, William, "Families of Functions." http://www.wmueller.com/precalculus/families/1_30.html (accessed 6/29/2010).