Parabolas
Parabolas
Nonstandard Form
If the equation is not given in standard form, it will need to be converted to standard form by completing the square. To identify an equation as a parabola, it will contain only one squared term as in the example below.
Example Convert the equation below to standard form. State which direction the parabola opens and determine its vertex, focus, directrix, and axis of symmetry.
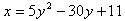
Example Convert the equation below to standard form. State which direction the parabola opens and determine its vertex, focus, directrix, and axis of symmetry.
Step 1 . Identify the conic section.
This is a parabola because there is only one squared term.
Step 2 . Write the equation in standard form.
Group the y terms and move the constant; x - 11 = (5y2-30y)
Factor the leading coefficient from the y group; x - 11 = 5(y2-6y)
Complete the square for y; x - 11 + (5?9) = 5(y2-6y+9)
Simplify; x = 5(y-3)2 - 34
Factor the leading coefficient from the y group; x - 11 = 5(y2-6y)
Complete the square for y; x - 11 + (5?9) = 5(y2-6y+9)
Simplify; x = 5(y-3)2 - 34
Step 3 . Identify the direction of opening, vertex, focus, directrix and the axis of symmetry.
This is a parabola that opens to the right because a > 0.
Vertex: (-34, 3)
Focus: 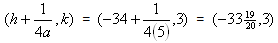
Equation of directrix: 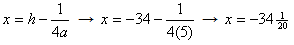
Axis of symmetry: