Print bookPrint book

Parabolas

Site: Clare-Gladwin RESD
Course: Michigan Algebra II KHauck
Book: Parabolas
Printed by: Guest user
Date: Sunday, 19 May 2024, 9:55 PM

Description

Parabolas

Table of contents

Parabolas

Parabolas were previously presented in function form. This book will introduce the conic section applications of parabolas. The connection to conic sections will not change the characteristics of parabolas. However some may seem new.

A parabola is the set of points in a plane that are the same distance from a given point and a given line in that plane. The given point is called the focus, and the line is called the directrix. The midpoint of the perpendicular segment from the focus to the directrix is called the vertex of the parabola. The line that passes through the vertex and focus is called the axis of symmetry.


Parabolas1
 

Opens Vertically

The equation of a parabola with vertex at (h, k) that opens in the "y-direction" is y = a(x - h)2 + k. The direction of opening is determined by the value of a. If a < 0, it will open down. If a > 0, it will open up. This form is exactly the same as a translated parabola from previous lessons. These parabolas will have the following properties:

Focus: OpensV1-1

Directrix: OpensV1-2

Axis of symmetry: OpensV1-3
 

Opens Horizontally

The equation of a parabola with vertex at (h, k) that opens in the "x-direction" is x = a(y - k)2 + h. The direction of opening is determined by the value of a. If a < 0, it will open to the left. If a > 0, it will open to the right. These parabolas will have the following properties:

Focus: OpensH1-1

Directrix: OpensH1-2

Axis of symmetry: OpensH1-3

Example 1

Graph the parabola below. State which direction the parabola opens and determine its vertex, focus, directrix, and axis of symmetry.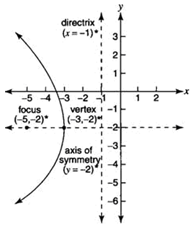

ParabolasEx1-1

Step 1 . Identify the direction of opening, vertex, focus, directrix and the axis of symmetry. This is a parabola that opens to the left because a < 0.

Vertex: (-3, -2)

Focus: ParabolasEx1-2

Equation of directrix: ParabolasEx1-3

Axis of symmetry: ParabolasEx1-4

Step 2. Graph the conic.
ParabolasEx1-5
>

Symmetry

Parabolas have reflectional symmetry, no rotational symmetry. The reflectional symmetry depends on the orientation of the parabola. If the parabola is vertical, then the line of symmetry is vertical through the vertex. If the parabola is horizontal, then the line of symmetry is horizontal through the vertex.

Example State the symmetry for the parabola modeled by the equation:

ParabolaRevised1

Step 1. State the vertex.

The vertex of the parabola is: (5, 2)

Step 2. State the reflectional symmetry.

This parabola has a horizontal line of symmetry at y = 2.

Step 3. State the rotational symmetry.

Parabolas do not have rotational symmetry.

Nonstandard Form

If the equation is not given in standard form, it will need to be converted to standard form by completing the square. To identify an equation as a parabola, it will contain only one squared term as in the example below.

Example Convert the equation below to standard form. State which direction the parabola opens and determine its vertex, focus, directrix, and axis of symmetry.

ParabolasEx2-1
Step 1 . Identify the conic section.

This is a parabola because there is only one squared term.

Step 2 . Write the equation in standard form.

Group the y terms and move the constant; x - 11 = (5y2-30y)

Factor the leading coefficient from the y group; x - 11 = 5(y2-6y)

Complete the square for y; x - 11 + (5?9) = 5(y2-6y+9)

Simplify; x = 5(y-3)2 - 34
Step 3 . Identify the direction of opening, vertex, focus, directrix and the axis of symmetry.

This is a parabola that opens to the right because a > 0.

Vertex: (-34, 3)

Focus: ParabolasEx2-2

Equation of directrix: ParabolasEx2-3

Axis of symmetry: ParabolasEx2-4

Video Lessons

To learn how to graph parabolas, select the following link:

Graph Parabolas

To learn how to write the equation of a parabola, select the following link:

Equation of a Parabola

Interactive Activity

Parabolas

Guided Practice

To solidify your understanding of graphing and writing equations of parabolas, visit the following link to Holt, Rinehart, and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.

Guided Practice

Practice

Parabola Worksheet
*Note: If Google Docs displays, “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Video Lesson: To see more examples on parabolas, view the video below.

Answer Key

Answer Key for Parabola Worksheet

*Note: If Google Docs displays, "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
 

Sources

Sources used in this book:

CliffsNotes.com. Parabola. 28 Jul 2010 <http://www.cliffsnotes.com/study_guide/topicArticleId-38949,articleId- 38942.html>.

Green, Larry. "The Standard and General Form of a Parabola." http://www.ltcconline.net/greenl/java/IntermedCollegeAlgebra/StandardGen eral/StandardGeneral.html (accessed 7/27/2010).

Holt, Rinehart & Winston, "Conic Sections ." http://my.hrw.com/math06_07/nsmedia/homework_help/alg2/alg2_ch10_05_ homeworkhelp.html (accessed 7/27/2010).

Kenny Felder, "Conic Concepts -- Circles," Connexions, March 22, 2010, http://cnx.org/content/m18245/1.3/.