Ellipses
Horizontal
The equation of an ellipse that is centered at (0, 0) and has its major axis along the x-axis has the following standard form:
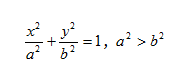
The length of the major axis is 2|a|, and the length of the minor axis is 2|b|. The endpoints of the major axis are (a, 0) and (?a, 0) and are referred to as the major intercepts or vertices. The endpoints of the minor axis are (0, b) and (0, -b) and are referred to as the minor intercepts or co-vertices. The points (c, 0) and (-c, 0) are the locations of the foci, and c can be found using the equation c2 = a2 - b2 . The key to understanding ellipses is understanding the three constants a, b and c.