Permutations & Combinations
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra II KHauck |
| Book: | Permutations & Combinations |
| Printed by: | Guest user |
| Date: | Monday, December 15, 2025, 6:08 AM |
Description
Fundamental Counting Principal
When trying to determine the total number of possible outcomes, it is sometimes hard to create the entire sample space either by organized list or by tree diagram. When this is true, it is helpful to use the fundamental counting principle. The fundamental counting principle states that when the outcomes of two or more events are independent, the total number of outcomes can be determined by multiplying the number of outcomes for each individual event.
Example A sandwich shop offers 5 kinds of bread, 8 types of meat and 6 cheeses. If you choose to make a sandwich with one item from each category, how many total possible sandwiches can you create?
Multiply the total outcomes from each category.
| Bread |
Meat |
Cheese |
||
| 5 |
x |
8 |
x |
6 |
There are 240 total possible sandwiches.
To learn more about the fundamental counting principle, select the following link:
Using the Fundamental Counting PrinciplePermutations
A permutation is an arrangement of objects in a certain order. The word arrangement is used, if the order of things is considered. An example of a permutation is selecting three students to be President, Vice President, and Secretary of the student council. The order in which they are selected will change the job they are given.
Permutations require the use of factorials, which are represented by the symbol "!". See the following example on how to apply the factorial symbol.
Factorial Example Find 6!
6! = 6?5?4?3?2?1 = 720
To do an activity that will help you develop the formula for permutations, select the following link:
Permutations Formula Worksheet
*Note: If Google Docs displays, “Sorry, we were unable to retrieve the document for viewing,†refresh your browser.
Discovery Answer Key
Once you have worked through the worksheet, select the following link to check your understanding:
Permutations Formula Answer Key
*Note: If Google Docs displays, “Sorry, we were unable to retrieve the document for viewing,†refresh your browser.
Example
How many different 7 player batting orders can be created from a 9 player team?
Step 1. Determine if this is a combination or a permutation.
Since the order the batters are in makes a difference, this is a permutation.
Step 2. Enter the data into the formula.
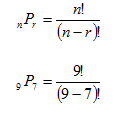
Step 3. Simplify the formula.
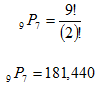
There are 181,440 different batting orders to choose from.
Video Lessons
To learn more about permutations, select the following link to a Holt, Rinehart & Winston video lesson:
To learn even more about permutations, watch the following video:
Practice
Permutation Worksheet*Note: If Google Docs displays, “Sorry, we were unable to retrieve the document for viewing,†refresh your browser.
Answer Key
Permutation Answer Key*Note: If Google Docs displays, “Sorry, we were unable to retrieve the document for viewing,†refresh your browser.
Combinations
A combination is a selection of objects in no particular order. The word selection is used, when the order of things has no importance. An example of a combination is selecting three students to be on the student council. Since no specific jobs are given, the order they are chosen will not change the members of the council.
To do an experiment that will help you develop the formula for combinations, select the following link:
Combinations Formula Worksheet
*Note: If Google Docs displays, “Sorry, we were unable to retrieve the document for viewing,†refresh your browser.
Discovery Answer Key
Once you have worked through the worksheet, select the following link to check your understanding:
Combinations Formula Answer Key
*Note: If Google Docs displays, “Sorry, we were unable to retrieve the document for viewing,†refresh your browser.
Example
How many different 5 player basketball teams can be selected from an 11 player team?
Step 1. Determine if this is a combination or a permutation.
Since the order of the players does not make a difference, this is a combination.
Step 2. Enter the data into the formula.
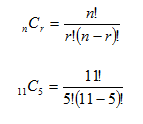
Step 3. Simplify the formula.
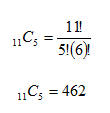
There are 462 different teams of 5 players to choose from.
Video Lesson
Practice
Combination Worksheet*Note: If Google Docs displays, “Sorry, we were unable to retrieve the document for viewing,†refresh your browser.
Answer Key
Combination Answer Key*Note: If Google Docs displays, “Sorry, we were unable to retrieve the document for viewing,†refresh your browser.
Combination vs. Permutation
To summarize, permutations are used when the order does matter and combinations are used when the order does not matter. The following formulas can be used to determine permutations and combinations:
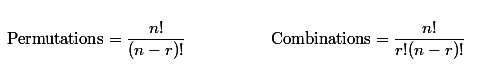
Video Lessons
To learn more about combinations vs. permutations, select the following link:
To learn how to use your TI-84 calculator to calculate combinations and permutations, watch the following video:
Guided Practice
To solidify your understanding of permutations and combinations, visit the following link to Holt, Rinehart, and Winston Homework Help Online. It provides examples, video tutorials, and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.
Sources
Sources used in this book:Brightstorm.com, "Combinations and Permutations Video." http://www.brightstorm.com/math/algebra-2/combinatorics/combinations-vs-permutations (accessed 7/27/2010).
Embracing Mathematics, Assessment & Technology in High Schools; a Michigan Mathematics & Science Partnership Grant Project
Holt, Rinehart & Winston, "Finding Permutations." http://my.hrw.com/math06_07/nsmedia/lesson_videos/alg2/player.ht ml?contentSrc=7199/7199.xml (accessed 7/28/2010).
Holt, Rinehart & Winston, "Probability & Statistics." http://my.hrw.com/math06_07/nsmedia/homework_help/alg2/alg2_ch 11_01_homeworkhelp.html (accessed 7/28/2010).
Holt, Rinehart & Winston, "Solving Combination Problems." http://my.hrw.com/math06_07/nsmedia/lesson_videos/alg2/player.ht ml?contentSrc=7200/7200.xml (accessed 7/28/2010).
Holt, Rinehart & Winston, "Using the Fundamental Counting Principal."http://my.hrw.com/math06_07/nsmedia/lesson_videos/alg2/player.ht ml?contentSrc=6490/6490.xml (accessed 7/28/2010).
Mathisfun.com, "Combinations and Permutations Calculator." http://www.mathsisfun.com/combinatorics/combinations-permutations- calculator.html (accessed 7/28/2010).