Print bookPrint book

Summation Notation

Site: Clare-Gladwin RESD
Course: Michigan Algebra II KHauck
Book: Summation Notation
Printed by: Guest user
Date: Tuesday, November 26, 2024, 12:35 AM

Description

Summation Notation

Table of contents

Summation Notation

Summation Notation is a mathematical notation for finding the sum of the terms of any sequence. The mathematical symbol for summation is the Greek letter sigma, Summation1-1 . In the previous book we used the following example to denote the sum of the first five terms of a sequence: Summation1-2. The notation that describes the summation of the first term through the fifth term of a sequence is summation1-3. Therefore, Summation1-4.

The notation for the sum of n terms is Summation1-5. In summation notation, the letter n is called the index of summation . The value below the sigma represents the initial term. The value above the sigma represents the final term. an represents the explicit formula for the sequence.

Example 1

Find the value of the following summation:
SumEx1-1
Step 1. Determine if the sequence is arithmetic or geometric.

The function representing the sequence is linear. Therefore the summation represents an arithmetic series.

Step 2. Determine a1 and an. For this example, the first term is a1and the last term is a47.
SumEx1-2 and SumEx1-3

Step 3. Determine the number of pairs.
SumEx1-4

Step 4. To find the series, substitute and solve.
SumEx1-5

SumEx1-6

SumEx1-7

Example 2

Find the value of the following summation: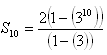
SumEx2-1
Step 1. Determine if the sequence is arithmetic or geometric.

The function representing the sequence is exponential. Therefore the summation represents a geometric series.

Step 2. Determine a1, r and n.
SumEx2-2, SumEx2-3, and SumEx2-4

Step 3. To find the series, substitute and solve.

SumEx2-5

SumEx2-6

SumEx2-7

SumEx2-8

SumEx2-9

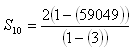
Example 3

Find the value of the following summation:
SumEx3-1

Step 1. Determine if the sequence is arithmetic or geometric.
The function representing the sequence is linear. Therefore, the summation represents an arithmetic series.

Step 2. Determine a1 and an. For this example, the first term is a15and the last term is a27.

SumEx3-2 and SumEx3-3

Step 3. Determine the number of pairs.

For this example, n = 15 is the first term and n = 27 is the last term. This means there are 13 terms in this series.

SumEx3-4

Step 4. To find the series, substitute and solve.
SumEx3-5

SumEx3-6

SumEx3-7

Video Lesson

To learn how to use summation notation, select the following link:

Summation Notation

Guided Practice

To solidify your understanding of summation notation, visit the following link to Holt, Rinehart, and Winston Homework Help Online. It provides examples, video tutorials, and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.

Guided Practice

Practice

Summation Notation Worksheet

*Note: If Google Docs displays. “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

To learn more about Summation Notation watch the video below.

 

Answer Key

Answer Key for Summation Notation Worksheet

*Note: If Google Docs displays, “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Sources

Sources used in this book:

Embracing Mathematics, Assessment & Technology in High Schools; a Michigan Mathematics & Science Partnership Grant Project

Florida Virtual School, http://www.flvs.net/ (accessed 2/25/2010).

Holt, Rinehart & Winston, "Sequence and Series." http://my.hrw.com/math06_07/nsmedia/homework_help/alg2/alg2_ch12_02_homeworkhelp.html (accessed 7/14/2010).

Stapel, Elizabeth. "Arithmetic and Geometric Sequences." http://www.purplemath.com/modules/series3.htm (accessed 2/25/2010).