Print bookPrint book

Geometric

Site: Clare-Gladwin RESD
Course: Michigan Algebra II KHauck
Book: Geometric
Printed by: Guest user
Date: Monday, 20 May 2024, 2:51 AM

Description

Table of contents

Geometric

A geometric sequence is a sequence that has a common multiplier between terms. This ratio is constant and is called the common ratio, r. The difference between consecutive terms in a geometric sequence varies, unlike an arithmetic sequence.

An example of a geometric sequence is 1, 2, 4, 8, 16 … and the common ratio of this sequence is 2. To change from one term to the next in the sequence, multiply by two.


Example 1

Find the common ratio of the following sequence:

geometric_ex1 - 1

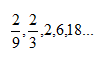
To find the common ratio, divide any consecutive pair of terms.

geometric ex1-2

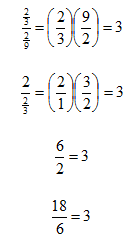
The ratio is always 3, or r = 3


Example 2

Write the first four terms of a sequence given that an = 3 · 2n-1 .

Step 1. Find the first term. To find the first term, a1, substitute the term number, n = 1 in the formula and solve.

a1 = 3·21-1

a1 = 3

Step 2. Find the second term. To find the second term, a2, substitute the term number, n = 2 in the formula and solve.

a2 = 3·22-1

a2 = 6

Step 3. Find the third term.

a3 = 3·23-1

a3=12

Step 4. Find the fourth term.

a4 = 3·24-1

a4 = 24

The first four terms of the sequence are 3, 6, 12, and 24.



Explicit Models

The following steps lead to an important discovery. Remember, when finding the next term in a geometric sequence, multiply by the common ratio, r.
First Term: a 1

Second Term: a 2 = a1?r

Third Term: a 3 = a2?r
= (a1?r)r = a1r2
Fourth Term: a 4 = a3?r
= (a1r2) r = a1r3
* Notice that in each term, the exponent on r is always one less than the position of the term: a4 = a1r(4-1) = a1r3 .

Nth Term: an = a1r n-1

The formula above is also known as the explicit formula and is used to determine the nth term when the previous term is unknown. When simplified, this formula becomes: explicit models and is exponential.


Example 1

Find the first four terms of a geometric sequence whose first term is 2 and whose common ratio is 4.

Step 1. Use the first term and the common ratio to find the terms.

2 x 4 = 8

8 x 4 = 32

32 x 4 = 128

Therefore, the first four terms are 2, 8, 32, and 128.

Example 2

Find the 15th term of a geometric sequence whose first term is 2 and whose common ratio is 4.

Step 1. Use the formula to determine the explicit model.

explicit ex 2 -1

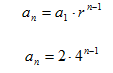
Step 2. Substitute the position of the term into the model and solve.

To find term 15, use n = 15.

explicit ex 2-2


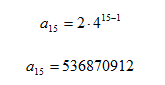
Example 3

Find the explicit model for the following sequence:

-1, -3, -9, -27 …

Step 1. Determine the common ratio.

explicit_ex3-1

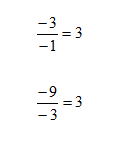
Every ratio will be three, r = 3.

Step 2. Substitute r = 3 and a1 = -1 into the formula and simplify.

explicit_ex3-2


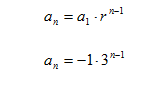
Example 4

Find the nth and the 26th terms of the geometric sequence with a5 = 5/4 and a12 = 160.

Step 1. These two terms are 12 - 5 = 7 places apart. Based on the definition of a geometric sequence stated earlier in this unit, a12 = ( a5 )( r7 ). Use this equation to solve for the value of the common ratio, r.

explicit_ex4-1

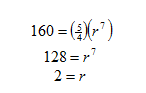
Step 2. Using information from one of the given terms, substitute and solve for a1.

explicit_ex4-2


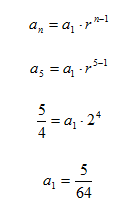
Step 3. Substitute a1 into the formula.

explicit_ex4-3

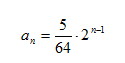
Step 4. Find the 26th term.

Substitute n = 26 into the formula and solve.

explicit_ex4-4

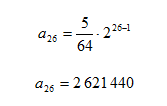
Compound Interest

Compound interest is interest paid on earned interest. The interest is paid on the principal and on the interest that has already been paid. Compound interest was discussed during the exponentials and logarithms unit. The process is based on a geometric sequence. The following example will develop a geometric sequence and an explicit formula for that sequence.

Example

Sara invested $1,000 in a savings account paying 4% interest compounded annually. Determine the amount of money Sara will have in the account at the end of the first five years.

Step 1. Determine the amount of money in the account after 1 year.

A 1 = 1000 + (.04)(1000)=1000 + 40= $1040

Step 2. Determine the amount of money in the account after 2 years.

A 2 = 1040 + (.04)(1040) = 1040 + 41.60 = $1081.60

Step 3. Use the pattern to determine the amount of money in the account after 3, 4, and 5 years.

A 3 = 1081.60 + (.04)(1081.60)=1081.60 + 43.26= $1124.86

A 4 = 1124.86 + (.04)(1124.86)=1124.86 + 44.99= $1169.85

A 5 = 1169.85 + (.04)(1169.85)=1169.85 + 46.79= $1216.64
Step 4. Create a geometric sequence to show the amount of money in the account after each of the 5 years.

1040, 1081.60, 1124.86, 1169.85, 1216.64

Step 5. Determine a1 and r for the sequence.

a 1 = 1040 and r = 1.04

Step 6 . Write an explicit formula for the geometric sequence.

an = 1040(1.04)n-1 or an= 1000(1.04) n

Notice this is the same formula used for compound interest in the Exponentials Unit. A = P(1 + r)t

Recursive Models

Another way to represent a geometric sequence is a recursive function, or any model that demonstrates how to find the next term in a sequence. In order to find the next term, an, multiply the previous term, an-1, by the common ratio. An example of a recursive model is: an = r · an-1 . This formula is also known as the recursive formula and is used when previous terms and the common ratio are known values.

Example Write a recursive function to model the following sequence:

3, 6, 12, 24, 48 …

Step 1. Determine the common ratio.

recursive-1

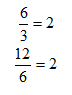
The common ratio is two, r = 2.

Step 2. Write a recursive model and reference the first term.

recursive-2



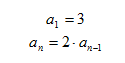
Video Lessons

To learn how to find common ratios, select the following link:

Identifying Geometric Sequences

To learn how to find the general formula for geometric sequences, select the following link:

Finding the nth Term in a Given Geometric Sequence

To learn how to find the nth term of geometric sequences, select the following link:

Finding the nth Term Given Two Terms




Interactive Activity

Geometric Sequences




Guided Practice

To solidify your understanding of geometric sequences, visit the following link to Holt, Rinehart, and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.

Guided Practice

Practice

Geometric Sequences Worksheet

*Note: If Google Docs displays, "Sorry, we were unable to retrieve the document for viewing," refresh your browser.

Video Lesson:


Answer Key

Geometric Sequences Answer Key

*Note: If Google Docs displays, "Sorry, we were unable to retrieve the document for viewing," refresh your browser.

Sources

Sources used in this book:

Embracing Mathematics, Assessment & Technology in High Schools; a Michigan Mathematics & Science Partnership Grant Project

Florida Virtual School, http://www.flvs.net/ (accessed 2/25/2010).

Holt, Rinehart & Winston, "Guided Practice." http://go.hrw.com/math/midma/gradecontent/loadlesson.html?course=c3&chapter=12&lesson=2&SE=1&sz_audio=1&calc=1&state=xx&actCourse=4 (accessed 7/14/2010).

Holt, Rinehart & Winston, "Sequences and Series." http://my.hrw.com/math06_07/nsmedia/homework_help/alg2/alg2_ch12_04_homeworkhelp.html (accessed 7/14/2010).

Ohio Department of Education, "Compounding the Problem - Grade 11." http://ims.ode.state.oh.us/ODE/IMS/Lessons/Web_Content/CMA_LP_S04_BC_L11_I02_01.pdf (accessed 8/10/2010).

Stapel, Elizabeth. "Arithmetic and Geometric Sequences." http://www.purplemath.com/modules/series3.htm (accessed 2/25/2010).