Print bookPrint book

Circles

Site: Clare-Gladwin RESD
Course: Michigan Algebra II KHauck
Book: Circles
Printed by: Guest user
Date: Saturday, May 18, 2024, 10:29 AM

Description

Table of contents

Circles

A circle is the set of all points in a plane that are the same distance from a given point. The point is known as the center of the circle, and the distance is known as the radius. In order to graph a circle, the center and radius must be known. If the equation of the circle is given in standard form, the graph is fairly simple to create. The standard form of the equation of a circle is:

circle

(h, k) is the center of the circle

r is the length of the radius

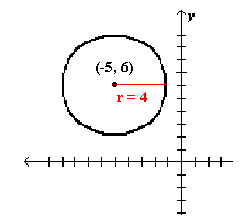
Example Graph (x+5)2 + (y-6)2 = 16.

Step 1 . Identify the center and radius.

center (-5, 6) radius = 4

Step 2. Graph the circle.

circle_ex1-1

Non-Standard Form

If the equation is not given in standard form, it will need to be converted to standard form by completing the square. To identify an equation as a circle, it will contain an x2 and y2 term with equal coefficients. See the following examples:

  • -3x2 - 3y2 + x - y = 5 is a circle.
  • 3x2 - 3y2 + x - y = 5 is not a circle.
  • 3x2 + 3y = 5 is not a circle.

Example

Graph 2x2 + 2y2 - 12x + 28y - 12 = 0.

Step 1 . Identify the conic section.

This is a circle because the x and y terms are both squared,
have the same coefficient, and are added.

Step 2 . Write equation in standard form.

x 2 + y2 - 6x + 14y - 6 = 0; divide by the coefficient 2

(x2-6x) + (y2+14y) = 6; Group the x terms, group the y terms, and move the constant

(x2 - 6x + 9) + (y2 + 14y + 49) = 6 + 9 + 49; complete the square for x and y

(x - 3)2 + (y + 7)2 = 64; Simplify

Step 3. Graph the conic.

Identify the center (3, -7)

Identify the radius r = 8

circles_ex2-1

Equations

When given the center and radius of a circle, substitute the values into the standard form. When the center or radius is not given, they will need to be found in order to write the equation of a circle.

Example 1 Find the equation for a circle with center at (15,-4) and with a radius of 8 units.

Substitute the center and radius into the standard form of a circle and simplify.

(x - (15))2 + (y - (-4))2 = 82

(x?15)2 + (y+4)2 = 64



Example 2

Find an equation for the circle centered at (-5, 12) and passing through the point (-2, 8).

Step 1. Find the length of the radius.

In this example, the distance formula is needed to determine the radius.

circles_ex3-1-fix

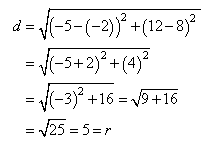
Step 2. Substitute the center and radius into the standard form of a circle and simplify.

(x - (-5))2 + (y - (12))2 = 52

(x + 5)2 + (y - 12)2 = 25

Symmetry

Circles have both reflectional and rotational symmetry. The reflectional symmetry of every circle is an infinite number of lines through the center point. The rotational symmetry of every circle is an infinite number of degrees about the center point.

Example State the symmetry for the circle modeled by the equation:

ConicsRevised1

Step 1. State the center.

The center of the circle is: (2, 4)

Step 2. State the reflectional symmetry.

This circle has an infinite number of lines of symmetry through the point (2, 4).

Step 3. State the rotational symmetry.

This circle has an infinite number of degrees of rotational symmetry around the point (2, 4).

Video Lessons

To learn how to graph circles, select the following link:

Graphing a Circle

To learn how to write the equation of a circle, select the following links:

Using Distance Formula to Write the Equation of a Circle

Writing the Equation of a Circle




Guided Practice

To solidify your understanding of graphing circles and writing equations of circles, visit the following links to Holt, Rinehart, and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.

Guided Practice 1

Guided Practice 2



Practice

Circles Worksheet

Finding the Center and Radius

*Note: If Google Docs displays, "Sorry, we were unable to retrieve the document for viewing," refresh your browser.



Video Lessons

Graphing a Circle in Standard Form


Equations for Circles in Standard Form





 

Answer Key

Circles Answer Key

Finding the Center and Radius Answer Key

*Note: If Google Docs displays, "Sorry, we were unable to retrieve the document for viewing," refresh your browser.



Sources

Sources used in this book:

Green, Larry. "Circle Applet." http://www.ltcconline.net/greenl/java/IntermedCollegeAlgebra/circleGraph/ circleGraph.htm (accessed 7/27/2010).

Holt, Rinehart & Winston, "Circles." http://my.hrw.com/math06_07/nsmedia/homework_help/geo/geo_ch11_07_h omeworkhelp.html (accessed 7/27/2010).

Holt, Rinehart & Winston, "Conic Sections ." http://my.hrw.com/math06_07/nsmedia/homework_help/alg2/alg2_ch10_02_ homeworkhelp.html (accessed 7/27/2010).

Kenny Felder, "Conic Concepts -- Circles," Connexions, March 22, 2010, http://cnx.org/content/m18245/1.3/.

Stapel, Elizabeth. "Conics: Circles: Working with Equations." Purplemath. Available from http://www.purplemath.com/modules/circle2.htm. Accessed 15 April 2010

WebMath, "Graph a Circle." http://www.webmath.com/gcircle.html (accessed 7/27/2010).