Overview
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra II KHauck |
| Book: | Overview |
| Printed by: | Guest user |
| Date: | Thursday, December 18, 2025, 12:08 PM |
Description
Overview
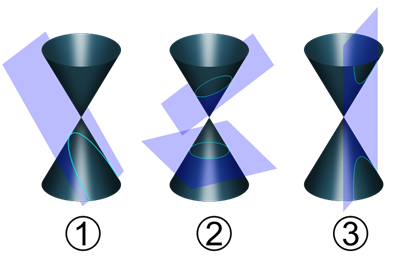
The shapes created by intersecting a plane with a double cone are called conic sections. This unit will discuss these shapes which include: parabolas, circles, ellipses, and hyperbolas. In diagram 1, the plane intersects one cone at an angle through one side of the cone creating a parabola. In the bottom half of diagram 2, the horizontal plane intersects one cone creating a circle. In the top half of diagram 2, the plane intersects one cone at an angle creating an ellipse. In diagram 3, the vertical plane intersects both cones creating a hyperbola.
In this unit you will learn the formal definition and formula of each conic. You will graph and explore applications of each shape.
Expectations
MI Alg2 High School Content Expectations
Addressed Within the Conics Unit.
L1.2.1 Use mathematical symbols to represent quantitative relationships and situations.
A2.4.3 Using the adapted general symbolic form, draw reasonable conclusions about the situation being modeled.
G.1.7.1 Find an equation of a circle given its center and radius; given the equation of a circle, find its center and radius.
G1.7.2 Identify and distinguish among geometric representations of parabolas, circles, ellipses, and hyperbolas; describe their symmetries, and explain how they are related to cones.
G1.7.3 Graph ellipses and hyperbolas with axes parallel to the x- and y-axes, given equations.
Sources
Source used in this book:Wikipedia, "Conic Section." http://en.wikipedia.org/wiki/Conic_section (accessed 7/27/2010).