Exponentials
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra II KHauck |
| Book: | Exponentials |
| Printed by: | Guest user |
| Date: | Tuesday, November 26, 2024, 12:23 AM |
Description
Growth & Decay
There are many applications of exponential functions. This book will discuss exponentials such as: population change, compound interest, half-life and doubling. The general form for all applications will be y = a.bx , where a is the initial value and b is the rate of growth or decay.
In the general form y = abx , b > 1 indicates exponential growth. Such applications include population growth and compound interest.
When b < 1, it indicates exponential decay. Such applications include population decline and half-life.
Application 1
Write an equation to model a population that starts at 100,000 and grows 3.5% per year.
Step 1. Determine the initial value. The population starts at 100,000.
a = 100000
Step 2. Write the rate as a growth factor. The population is growing by 3.5%, add this to 100%. 100% + 3.5% = 103.5%, translated to a decimal 1.035
b = 1.035
Step 3. Write the equation.
y = a . bx
y = 100000(1.035)x
Application 2
Write an equation to model bacterial growth. Assume the bacteria starts with 5 bacteria and doubles every 12 hours.
Step 1. Determine the initial value. The population starts at 5 bacteria.
Step 2. Write the rate as a growth factor. The population doubles.
for every 12 hours.
Step 3. Alter the exponent to include the doubling time of 12 hours. Recall that b is the common ratio as the input goes up by one and that roots can be rewritten as rational exponents. This input is going up by 12; therefore take the 12th root of 2 to simplify the expression.
Step 4. Write the equation.
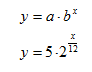
Application 3
A certain population of eagles starts at 50, but is declining by 4% per year. Write an equation to model this population.
Step 1. Determine the initial value. The population starts at 50 eagles.
a = 50
b = 0.96
Step 3. Write the equation.
y = a . bx
y = 50(0.96)x
Application 4
A certain chemical compound has a half-life of 14 days. Currently there is 45 mg of the compound. Write an equation to model the half-life of this compound.
Step 1. Determine the initial value. The compound starts with 45 mg.
Step 2. Write the rate as a decay factor. The chemical has a half-life.
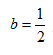for every 14 days
Step 3. Alter the exponent to include the half-life of 14 days. This input is going up by 14; therefore take the 14th root of ½ to simplify the expression.
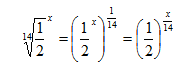
Step 4. Write the equation.
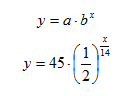
Video Lesson
To learn how to solve problems involving exponential growth or decay, select the following link:
Exponential Growth or Decay
Compound Interest
Compound Interest is a form of an exponential equation used in finance. In the compound interest formula, a is the initial value invested or borrowed, b is the interest rate, and x is the number of years the loan is compounded. For this application, the general form becomes A = P(1+r)t :
- A is the total amount
- P is the principle (initial) amount invested or borrowed
- r is the annual interest rate in decimal form
- t is the time in years
Application 5
You would like to buy a new car that costs $20,000. Since you have not saved enough money, you will need to take out a loan. The bank is offering a loan at 5% annual interest. What equation will model this loan?
Step 1. Determine P. The initial amount borrowed is 20,000
P = 20000
Step 2. Determine r. The interest rate is 5%.
r = 0.05
Step 3. Write the equation.
A = P(1+r)t
A = 20,000(1+0.05)t
A = 20,000(1.05)t
Application 6
You were given $100 for your birthday. You choose to put the money in an interest-bearing account that earns 4.5% interest compounded quarterly. What equation will model the total amount of money in the account?
*Note: When the interest is compounded more than once per year, the formula becomes 
; 
represents the portion of interest earned for each compounding cycle, 
represents the number of compounding cycles.
Step 1. Determine P. The initial amount is 100.
Step 2. Determine nt. The interest rate is 4.5% compounded quarterly. Therefore, the rate must be divided into 4 equal parts.
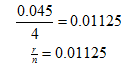
Step 3. Determine nt. The interest is compounded quarterly; therefore n = 4.
Step 4. Write the equation.
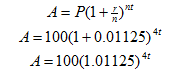
Compounded Continuously
One other type of compound interest is when interest is compounded continuously. This formula involves the constant e and has the form A = Pert , where all variables mean the same as in the previous application.
Application 7 You invest $500 in a stock that compounds continuously at a rate of 2.5%. Write an equation to model this situation.
Step 1. Determine P. The initial amount invested is $500.
P = 500
Step 2. Determine r. The interest rate is 2.5%.
r = 0.025
Step 3. Write the equation.
A = Pert
A = 500e0.025t
Video Lesson
To learn how to solve problems that are compounded continuously, select the following link:
Practice
Interest Rate Problems Worksheet
Answer Keys
Sources
Sources used in this book:Embracing Mathematics, Assessment & Technology in High Schools; a Michigan Mathematics & Science Partnership Grant Project
"Exponential Growth in the Real World." http://www.mathwarehouse.com/exponential-growth/exponential- models-in-real-world.php (accessed 7/14/2010).
Holt, Rinehart & Winston, "Economics Applications." http://my.hrw.com/math06_07/nsmedia/lesson_videos/alg2/player.ht ml?contentSrc=7155/7155.xml (accessed 7/14/2010).
Holt, Rinehart & Winston, "Exponential Applications." http://my.hrw.com/math06_07/nsmedia/lesson_videos/alg2/player.ht ml?contentSrc=7136/7136.xml (accessed 7/14/2010).
Marcus, Nancy. "Applications of Exponential and Logarithmic Equations." http://www.sosmath.com/algebra/logs/log5/log51/log51.html (accessed 7/14/2010).