Exponentials
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra II KHauck |
| Book: | Exponentials |
| Printed by: | Guest user |
| Date: | Tuesday, November 26, 2024, 12:38 AM |
Description
Growth
The exponential parent function is y = kx where k is a constant. The easiest way to begin looking at this pattern is to make a table.
Recall from the Families of Functions Unit that the function g(x) = 2x would create the following table and graph:
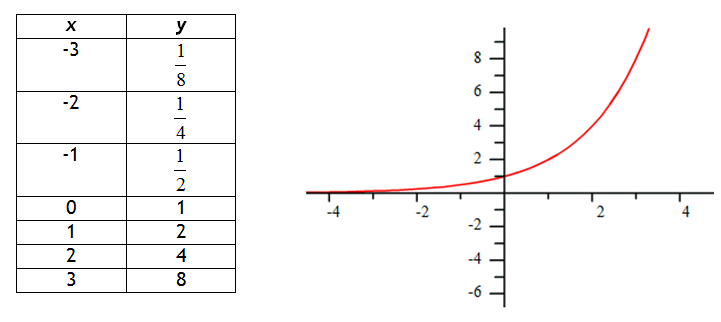
Notice that the graph increases more rapidly as x increases. The left side of the graph is approaching, but never touches the line y = 0, which is the graph's asymptote. Therefore, the domain of this function is 
and the range of the function is 
.
Decay
Recall that the function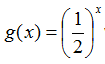 
would create the following table and graph:
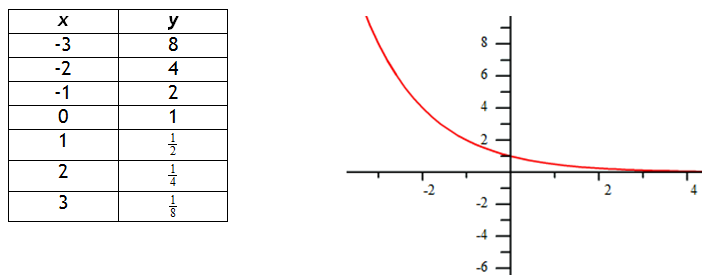
Notice that the graph decreases more rapidly as x increases. The right side of the graph is approaching, but never touches the line y = 0, which is the graph's asymptote. Therefore, the domain of this function is 
and the range of the function is 
.
Video Lesson: Graphing
Interactive Activity
Transformations
The transformations of functions that were presented in the Families of Functions unit also apply to exponential functions. The following list shows how the patterns apply to exponentials:
1. y = 2 x + a translates the graph a units up; asymptote equation y = a
2. y = 2 x -a translates the graph a units down; asymptote equation y = -a
3. y = 2 x-a translates the graph a units right; asymptote equation y = 0
4. y = 2 x+a translates the graph a units left; asymptote equation y = 0
5. y=-(2 x) reflects the graph across the x-axis; asymptote equation y = 0
6. y = 2 -x reflects the graph across the y-axis; asymptote equation y = 0
Video Lessons
To learn how to transform exponential graphs, select the following link:
Translating Exponential Functions
To learn more about transforming exponential graphs, select the following link:
Stretching, Compressing & Reflecting Exponential Functions
Video Lesson:
To see more examples on exponential transformations, view the video below.
Identifying
Exponential Functions follow the form y = abx where a is the y-intercept and b is the common ratio of the table. When modeling exponential data the a-value is the y-intercept, therefore find the point where x = 0. To determine the b-value calculate the common ratio between consecutive y-values.
Video Lesson
To learn how to identify exponential data, select the following link:
Modeling A Graph
In order to write the function that models an exponential graph, find at least two points on the graph. If the y-intercept (0, a) is easily determined, select it as one of the two points. Otherwise, select two points with integer coordinates to make the computation easier. Then calculate the a and b-values.
Example Write a function to model the graph.
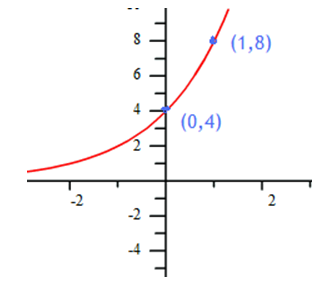
Step 1. Determine the y-intercept.
Notice (0, 4) is on the graph, therefore a = 4 and y = 4 . bx
Step 2. Determine another point on the graph and substitute it into x and y in the equation, then solve for b.
Notice (1, 8) is on the graph, use it in the equation.
8 = 4 . b1
2 = b
Therefore, y = 4 . 2x models this graph.
Modeling Points
When given two or more points of an exponential graph, try one of the following methods:
- If the y-intercept is one of the points, the model can be found exactly like the previous example.
- If the y-intercept is not given, put the points into a table and find the common ratio.
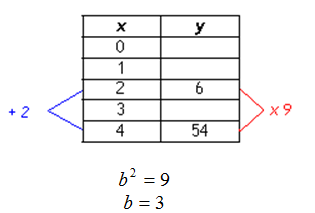
Example Find the exponential function that models the points (2, 6) and (4, 54)
Step 1. Put the points into a table.
| x |
y |
| 0 |
|
| 1 |
|
| 2 |
6 |
| 3 |
|
| 4 |
54 |
Step 2. Find the common multiplier between the y-values.
6 . __ = 54
6 . 9 = 54
Example Continued
Step 3. Find the common ratio.
The common ratio is based on x-values with an increment of 1. If the increment is not 1, then set up the equation
b x-increment = common multiplier and solve for b.
Step 5. Write the exponential model.
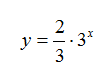
Guided Practice
To solidify your understanding of identifying and modeling exponential data, visit the following link to Holt, Rinehart, and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.
Guided PracticePractice
Graphing Exponential Functions Worksheet
*Note: If Google Docs displays, "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Answer Key
*Note: If Google Docs displays, "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Sources
Sources used in this book:Edwards, P. "The Exponential Function Applet." http://mathinsite.bmth.ac.uk/applet/exponential/exp.html (accessed 7/13/2010).
Embracing Mathematics, Assessment & Technology in High Schools; a Michigan Mathematics & Science Partnership Grant Project
"Exponential Growth Equations and Graphs ." http://www.mathwarehouse.com/exponential-growth/graph-and- equation.php (accessed 7/13/2010).
Holt, Rinehart & Winston, "Exponential and Logarithmic Functions." http://my.hrw.com/math06_07/nsmedia/homework_help/alg2/alg2_ch 07_08_hom eworkhelp.html (accessed 7/13/2010).
Holt, Rinehart & Winston, "Identifying Exponential Data." http://my.hrw.com/math06_07/nsmedia/lesson_videos/alg2/player.ht ml?contentSr c=6468/6468.xml (accessed 7/13/2010).
Holt, Rinehart & Winston, "Transformations of Exponential Functions." http://my.hrw.com/math06_07/nsmedia/lesson_videos/alg2/player.ht ml?contentSr c=7157/7157.xml (accessed 7/13/2010).
Holt, Rinehart & Winston, "Translating Exponential Functions." http://my.hrw.com/math06_07/nsmedia/lesson_videos/alg2/player.ht ml?contentSr c=6467/6467.xml (accessed 7/13/2010).