Properties
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra II KHauck |
| Book: | Properties |
| Printed by: | Guest user |
| Date: | Tuesday, November 26, 2024, 12:47 AM |
Description
<b></b>
Properties
Logarithms are exponents, and therefore log properties are exponent properties. Using these properties makes it possible to simplify logarithmic expressions and solve logarithmic equations.Any base to the power of 0 equals 1. Inversely, the log of one is always zero.
or 
Product of Powers
When multiplying two exponents with the same base, keep the base and add the exponents.
Applied to Exponents: 
Applied to Logs: 
or 
Quotient of Powers
When dividing two exponents with the same base, keep the base and subtract the exponents.Applied to Exponents:
Applied to Logs:
or 
Power to a Power
When raising a power to a power, keep the base and multiply the exponents.Applied to Exponents:
Applied to Logs:
or 
Product to a Power
To raise a product to a power, raise each factor to the power.Applied to Exponents:
Applied to Logs:
Examples
Example 1 Use the properties of logs to simplify the expression:
Since this expression involves adding two exponents, Product of a Power Property will be used.
Example 2 Use the properties of logs to simplify the expression:
Step 1. Use the properties of logs to eliminate the coefficient.
Since this expression involves multiplying a number by an exponent, Power to a Power Property will be used.
Step 2. Simplify to one log.
Since this expression involves subtracting two exponents, Quotient of a Power Property will be used.
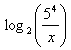
Video Lessons
To learn how to use the properties of logs to simplify expressions, select the following link:Properties to Simplify Log Expressions
To learn more about the properties of logs, select the following link:
Additional Properties of Logs
Change of Base Property
The Change of Base Property allows you to solve logs with a calculator when you cannot use mental math or conversion to exponential form. Since most scientific calculators only calculate common log
and natural log 
, there will be times when it is necessary to change bases in order to calculate a log function. The Change of Base Property states:
This is not a property that needs to be memorized; it can be found using the properties you have already learned as shown in the following example.
Example
Solve the equation:
Step 1. If it is not possible to create a common base, use the inverse function (logs). When applying inverses to an equation, do the same operation on both sides of the equals sign.
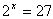
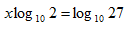
Step 2.Use properties of logs to eliminate the exponent.
Use the Power to a Power Property to multiply the exponent (x) by the exponent (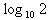
)
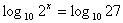
Step 3.Solve for x.
Use the Change of Base Property & divide.
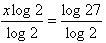
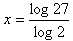
Step 2.
Use the Power to a Power Property to multiply the exponent (x) by the exponent (
) Step 3.
Use the Change of Base Property & divide.
x = 4.755 (using a calculator)
Therefore,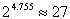 
Video Lesson
To learn how to apply the change of base property, view the video below.Common Mistakes
The most common mistakes made when using the log properties:
Interactive Activity
Online Simplifying Logs PracticeGuided Practice
To solidify your understanding of log properties, visit the following link to Holt, Rinehart, and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.Guided Practice
Practice
Properties of Logs*Note: If Google Docs displays, “Sorry, we were unable to retrieve the document for viewing,†refresh your browser.
To see more examples of the properties of logarithms, view the video below.
Answer Key
Answer Key for Properties of Logs Worksheet*Note: If Google Docs displays, “Sorry, we were unable to retrieve the document for viewing,†refresh your browser.
Sources
Sources used in this book:Embracing Mathematics, Assessment & Technology in High Schools; a Michigan Mathematics & Science Partnership Grant Project
Holt, Rinehart & Winston, "Exponential and Logarithmic Functions." http://my.hrw.com/math06_07/nsmedia/lesson_videos/alg2/player.html?contentSrc=6463/6463.xml (accessed 7/12/2010).