Inverse Functions
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra II KHauck |
| Book: | Inverse Functions |
| Printed by: | Guest user |
| Date: | Tuesday, November 26, 2024, 12:46 AM |
Description
Inverse Functions
Review of Exponential Functions
An exponential function is a function that has the variable as the power rather than the base. For example,
where the base is a constant and the power is a variable. Recall from Algebra I that the function
would create the following table and graph:
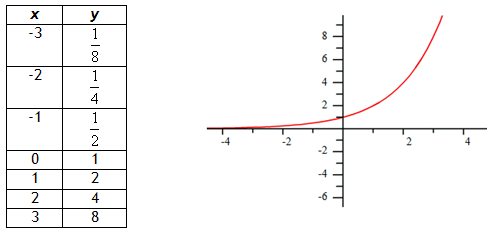
Guided Practice
To solidify your understanding of exponential functions, visit the following link to Holt, Rinehart, and Winston Homework Help Online. It provides examples, video tutorials, and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.Guided Practice
Introduction to Logarithms
Logarithmic functions and exponential functions are inverse functions. When two functions are inverses, switch the x and y coordinates. A logarithmic function is written in the form:
. The definition of logarithm states:
This definition allows you to convert between logarithmic and exponential equations because the two statements above are equivalent. In other words, a log is another way to write an exponent.
One of the keys in using this definition is to remember that when converting between logarithmic and exponential forms, the base is always the same. In the example above, the base of both functions is b.
Examples
Example 1Using the definition of logarithms, convert the following logarithmic equation to an exponential equation:
log4x = 2
If 
then 
or x = 16.
25 = 52
If 25 = 52 then
log9 x = ½
If log9 x = ½ then x = 9(1/2) and x =
and x = 3
then or x = 16. Example 2
Using the definition of logarithms, convert the following exponential equation to a logarithmic equation:
25 = 52
If 25 = 52 then
Example 3
Using the definition of logarithms, convert the following logarithmic equation to an exponential equation:
log9 x = ½
If log9 x = ½ then x = 9(1/2) and x =
and x = 3Video Lessons
To learn how to convert from exponential to log form, select the following link:Exponential to Log Form
To learn how to convert from log to exponential form, select the following link:
Log to Exponential Form
Common Log
A common log is a log with the base of 10. Because it is a common log, the base is not usually included when discussing this log. The common log is one of two logarithms that a scientific calculator will calculate.Example
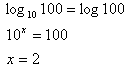
Natural Log
Natural log, abbreviated ln, is equivalent to
where e is a constant like 
and occurs in exponential applications. Natural log is the other log that a scientific calculator will calculate. Example
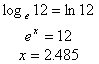
Evaluating Logs
To evaluate a logarithmic expression, convert to its corresponding exponential form and solve.
Example Evaluate
Step 1. Convert the log to its equivalent exponential form.
Step 2. Solve for x by rewriting 16 as a power with a base of 2.
Step 3. Substitute 24 in for 16 in step 1.
Step 4. Now that the bases are equal, set the exponents equal to each other.
Video Lessons
To see more examples on converting and evaluating logs, view the video below.Guided Practice
To solidify your understanding of logarithmic functions, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.Guided Practice
Practice
Exponential and Logarithmic Functions Worksheet*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing.†refresh your browser.
Answer Key
Answer Key for Exponential and Logarithmics Worksheet*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing.†refresh your browser.
Sources
Sources used in this book:Embracing Mathematics, Assessment & Technology in High Schools; a Michigan Mathematics & Science Partnership Grant Project
Holt, Rinehart & Winston, "Exponential and Logarithmic Functions." http://my.hrw.com/math06_07/nsmedia/lesson_videos/alg2/player.ht ml?contentSrc=6462/6462.xml (accessed 07/07/2010).
Holt, Rinehart & Winston, "Sequences and Functions." http://my.hrw.com/math06_07/nsmedia/homework_help/msm3/msm3_ch13_05_homeworkhelp.html (accessed 06/30/2010).
"Logarithms." http://www.mathsisfun.com/algebra/logarithms.html (accessed 7/12/2010).
Spector, Lawrence. "Logarithms." http://www.themathpage.com/alg/logarithms.htm (accessed 7/12/2010).