Transformations

Asymptotes

A vertical asymptote is a vertical line that the graph of the function approaches but never intersects. They are similar to horizontal asymptotes of exponential functions studied in Algebra I. The equation of a vertical asymptote has the form x = k, where k stands for a constant value.

A horizontal asymptote is a horizontal line that the graph of the function approaches, but unlike vertical asymptotes the graph can cross horizontal asymptotes. Horizontal asymptotes help to determine the end behavior of the graph of rational functions.

Parent Function

The simplest rational function is called the parent function and is . To understand how to graph a rational function, it is important to understand the shape of the parent function and how it moves. The graph of is shown below:

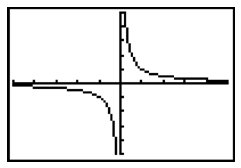
The parent function has an excluded value of x = 0. Notice that the graph approaches, but never touches the line x = 0, because the function is undefined at that value. This creates a vertical asymptote on the y-axis.

There is also a horizontal asymptote on the x -axis. There is no value of x , for which will equal 0. Therefore, as the value of x increases the value of the fraction approaches zero, creating the asymptote at y = 0.

Video Lesson

To learn how to graph transformations of select the following link:

Graph Transformations

Writing Equations

Writing a rational function can be accomplished by adding the asymptote lines to the parent function . It can also be done by using the rules of transformations.

Example 1 The graph below has a vertical asymptote at x = 2 and a horizontal asymptote at y = -4. What is the equation of the function that models this graph?

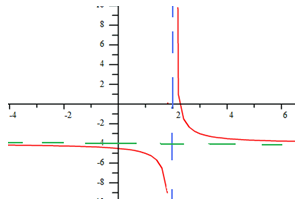
Example 2

The graph below is translated 5 left and 3 up from the parent function . Write an equation to model this graph.

Step 1. Use the rules of transformations to change the x-variable.

Step 2 . Use the rules of transformations to change the y-variable.

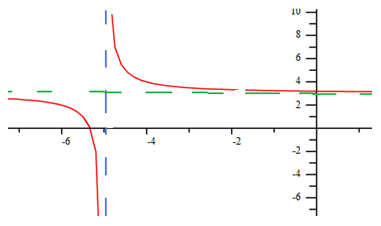
Practice

Rational Transformations Worksheet

Answer Key

Answer Key for Rational Transformations Worksheet

Sources