Solutions
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra II KHauck |
| Book: | Solutions |
| Printed by: | Guest user |
| Date: | Monday, December 29, 2025, 1:19 AM |
Description
Solutions of Rational Equations
Introduction
A rational equation is an equation containing rational expressions.
Examples of rational equations:
![]()
Solving Using LCDs
One way of solving rational equations is to multiply all terms in the equation by the least common denominator (LCD). Then simplify the products, eliminating the denominators.
Example 1 Solve.
![]()
Step 1. Find the LCD:
12 is the LCD because it is the least common multiple of 12, 3, and 4.
Step 2. Multiply each term by the LCD:
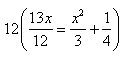
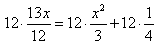
![]()
Step 3. Set the equation equal to zero.
![]()
Step 4. Solve by factoring and use the Zero Product Property.
![]() or
or![]()
![]() or
or ![]()
*Remember: you can always check your answers by plugging the solutions into the original equation.
Example 2
Solve.
![]()
Step 1. Factor all denominators.
![]()
Step 2. Find the LCD.
![]() is the LCD because it is the least common multiple of the three denominators
is the LCD because it is the least common multiple of the three denominators
{(x + 2),(x – 5), and (x+2)(x-5)}.
Step 3. Multiply all terms in the equation by the LCD.
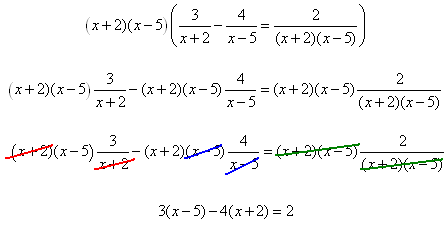
Step 4. Simplify and solve the resulting polynomial equation.
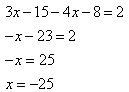
*Remember: you can always check your answers by plugging the solutions into the original equation.
Extraneous Solutions
Earlier in this unit there was an explanation of excluded values. These values are important to the solution of rational equations. After solving a rational equation, be sure the solution is not an excluded value.
Example 1 This IS an extraneous solution.
The solution to ![]() is x = 1, but x = 1 is an excluded value of the original equation, so x = 1 is an extraneous solution and not a member of the solution set. This rational equation has no solution.
is x = 1, but x = 1 is an excluded value of the original equation, so x = 1 is an extraneous solution and not a member of the solution set. This rational equation has no solution.
Example 2 This IS NOT an extraneous solution.
The solution to ![]() is x = -25. The excluded values of the original equation were
is x = -25. The excluded values of the original equation were ![]() , so x = -25 is a member of the solution set.
, so x = -25 is a member of the solution set.
Solving Using Cross Products
A rational equation that contains two terms, a proportion, is easily solved by the method of cross products or cross multiplication. This turns a rational equation into a polynomial equation.
Example 1 Solve.
![]()
Step 1. Use cross-multiplication to turn the rational equation into a polynomial equation.
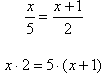
Step 2. Solve the equation.
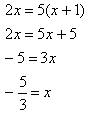
Step 3. Check for extraneous solutions.
The original equation had no excluded values, so ![]() is not an extraneous solution.
is not an extraneous solution.
*Remember: you can always check your answers by plugging the solutions into the original equation.
Example 2
Solve.
Step 1. Use cross-multiplication to turn the rational equation into a polynomial equation.
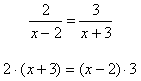
Step 2. Simplify the equation, using the distributive property.
Step 3. Solve the equation.
Step 4. Check for extraneous solutions.
The original equation had excluded values ![]() , since neither of these are the solution, x = 12 is not an extraneous solution.
, since neither of these are the solution, x = 12 is not an extraneous solution.
*Remember: you can always check your answers by plugging the solutions into the original equation.
Video Lesson
Guided Practice
To solidify your understanding of solving rational equations, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.
Practice
*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing.†refresh your browser.
Answer Key
Answer Key for Solving Rational Worksheet
*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing.†refresh your browser.
Sources
Sources used in this book:CK12, "Algebra I." 2009.http://ck12.org/flexr/viewer/962d35c81e3e9e1f4a10fdb462386484/ (accessed 06/23/2010).
Embracing Mathematics, Assessment & Technology in High Schools; a Michigan Mathematics & Science Partnership Grant Project
Holt, Rinehart & Winston, "Rational Functions & Equations." 2009.http://my.hrw.com/math06_07/nsmedia/homework_help/alg1/alg1_ch12_07_homeworkhelp.html (accessed 06/23/2010).