Multiplication
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra II KHauck |
| Book: | Multiplication |
| Printed by: | Guest user |
| Date: | Sunday, 19 May 2024, 4:32 PM |
Description
Multiplying
Multiplying Fractions
Remember when multiplying fractions, multiply the numerators (tops), and then multiply the denominators (bottoms). For instance, 
. Notice that 
can be simplified, since 7 divides evenly into the numerator and denominator, 
. So 
is the correct answer, but can be simplified to be 
.
To avoid working with larger numbers, simplify first. Notice that there is a factor of 7 in the numerator and denominator, which can be cancelled before multiplying.
Cancelling before multiplying is a great time-saver and prevents many common mistakes.
Hint: If the same factor appears in the numerator and the denominator, cancel it before multiplying. This works regardless of whether the numbers appear in the same fraction or different fractions.*Caution: This rule only applies when you are multiplying fractions; not when you are adding, subtracting, or dividing.
Multiplying Rational Expressions
The review of multiplying fractions is useful because multiplying rational expressions works the same way. You will also need to use the steps from simplifying rational expressions.
Example Multiply the following rational expression.
Step 1. Factor completely. (Factor a 3 out of the trinomial, and then factor the trinomial and the remaining expressions).
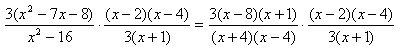
Step 2. Cancel the common factors (even across different fractions).
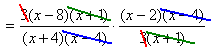
Step 3. Rewrite.
(Answer)
*Note: the numerator could be written as 
, but it is easier to work with in factored form.
Video Lesson
To learn how to Multiply Rationals select the following link to Holt, Rinehart and Winston :
Multiplying Rationals
Dividing Fractions
To divide fractions, multiply the first fraction by the reciprocal of the second fraction. To find the reciprocal of a fraction, flip the fraction over so that the denominator becomes the numerator and vice versa. After the “flipping†stage, all the considerations are exactly the same as multiplying fractions.
Example 
Remember: 
is the same as 
. At this level of math the ÷ symbol is rarely used.
Dividing Rational Expressions
The review of dividing fractions is useful because dividing rational expressions works the same way. You will also need to use the steps from simplifying rational expressions.
Example
Divide and simplify the following rational expression.
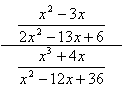
Step 1.Multiply the expression in the numerator by the reciprocal of the expression in the denominator.
Step 2. Factor completely.
Step 3. Cancel common factors.
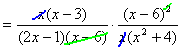
Step 4. Rewrite.
(Answer)
Video Lesson
To learn how to Divide Rationals select the following link to Holt, Rinehart and Winston :
Dividing Rationals
Guided Practice
To solidify your understanding of simplifying, multiplying and dividing rational expressions, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.
Practice
Multiplying Rational Expressions Worksheet
Answer Key
Multiplying Rational Expressions Answer Key
Sources
Sources used in this book:Embracing Mathematics, Assessment & Technology in High Schools; a Michigan Mathematics & Science Partnership Grant Project
Holt, Rinehart, & Winston, "Rationals & Radicals." http://my.hrw.com/math06_07/nsmedia/homework_help/alg2/alg2_ch08_02_homeworkhelp.html (accessed 6/16/2010).
Kenny Felder, "Rational Expression Concepts -- Multiplying Rational Expressions," Connexions, November 15, 2008, http://cnx.org/content/m18301/1.1/.