Division
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra II KHauck |
| Book: | Division |
| Printed by: | Guest user |
| Date: | Sunday, December 28, 2025, 3:11 PM |
Description
Division
In order to divide complex numbers, write the problem in fractional form. Because ![]() , when dividing complex numbers there is a radical sign in the denominator of the fraction and it is therefore necessary to rationalize the denominator.
, when dividing complex numbers there is a radical sign in the denominator of the fraction and it is therefore necessary to rationalize the denominator.
The purpose of rationalizing the denominator is to eliminate the radical sign in the denominator. In complex numbers this is achieved by using conjugates. The conjugate of a complex number a + bi is the complex number a - bi. For example, the conjugate of 4 + 2i is 4 - 2i. Notice that only the sign of the bi term is changed. The conjugate of 4i + 3 is not 4i - 3, but -4i + 3 because the sign on the bi term must change, not the a term.
Example 1
Simplify the expression
![]()
Step 1. Rewrite the expression as a fraction.
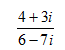
Step 2. Rationalize the denominator by multiplying the numerator and denominator by the conjugate.
![]()
Step 3. Use Distributive Property to multiply the complex numbers.
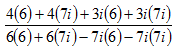
Step 4. Simplify.
![]()
Example 2
Simplify the expression
![]()
Step 1. Rewrite the expression as a fraction.
![]()
Step 2. Rationalize the denominator by multiplying the numerator and denominator by the conjugate.
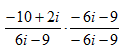
Step 3. Use Distributive Property to multiply the complex numbers.
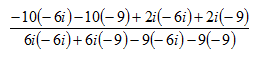
Step 4. Simplify.
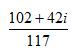
Application
To see an application of complex numbers, select the following link:
Complex Number ApplicationVideo Lesson
To learn how to simplify complex numbers using conjugates select the following link:
Guided Practice
To solidify your understanding of complex numbers, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.
Complex NumbersPractice
Dividing Complex Numbers Worksheet*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing." refresh your browser.
Answer Key
Dividing Complex Numbers Key*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing." refresh your browser.
Sources
Sources used in this book:
Bourne, M. "An Application of Complex Numbers: AC Circuits." 1/19/2009.http://www.intmath.com/Complex-numbers/8_AC-circuit-definitions.php (accessed 8/10/2010).
Embracing Mathematics, Assessment & Technology in High Schools; a Michigan Mathematics & Science Partnership Grant Project
Holt, Rinehart & Winston, "Quadratic Functions." http://my.hrw.com/math06_07/nsmedia/homework_help/alg2/alg2_ch05_09_homeworkhelp.html (accessed 8/10/2010).
Roberts, Donna. "Practice Multiplying and Dividing Complex Numbers." http://www.regentsprep.org/Regents/mathb/3C4/multprac.htm (accessed 8/10/2010).