Modeling
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra II KHauck |
| Book: | Modeling |
| Printed by: | Guest user |
| Date: | Wednesday, January 7, 2026, 6:12 PM |
Description
Modeling
To model a polynomial, work the steps to finding the x-intercepts of a polynomial backwards. First, determine the zeros of the function by looking at the table or graph. Second, turn each zero into a factor of the function. Finally, determine the factored form of the polynomial.
Example 1
Determine the function that models the table below:

Step 1. Determine the zeros of the function.
(-5, 0), (1, 0), (3, 0)
Step 2. Turn each zero into a factor of the function.
Since x = -5, then (x + 5) is a factor of the polynomial.
Since x = 1, then (x - 1) is a factor of the polynomial.
Since x = 3, then (x - 3) is a factor of the polynomial.
Step 3. Determine the factored form of the polynomial.
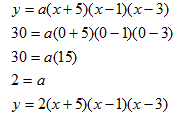
Example 2
Determine the function that models the graph below:

Step 1. Determine the zeros of the function.
(-1, 0), (0, 0), (5, 0)
Step 2. Turn each zero into a factor of the function.
Since x = -1, then (x + 1) is a factor of the polynomial.
Since x = 0, then (x) is a factor of the polynomial.
Since x = 5, then (x - 5) is a factor of the polynomial.
Step 3. Determine the factored form of the polynomial.
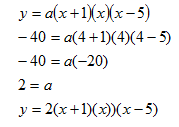
Additional Lesson
To learn more about writing polynomials from the zeros of the function, select the following link:
Practice
Modeling Polynomials Worksheet*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Answer Key
Modeling Polynomials Answer Key*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Sources
Sources used in this book:Ahrens, Judy. "Zeros of polynomial functions." 3/4/2000.http://www.pstcc.edu/facstaff/jahrens/math1130/polyroot.pdf
Embracing Mathematics, Assessment & Technology in High Schools; a Michigan Mathematics & Science Partnership Grant Project