Finding Intercepts
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra II KHauck |
| Book: | Finding Intercepts |
| Printed by: | Guest user |
| Date: | Tuesday, December 23, 2025, 6:04 PM |
Description
Finding Zeros
In order to graph a polynomial function, knowing where the graph crosses the x-axis is necessary. The value(s) of the x-intercept(s) are the zero(s) or real root(s) of the function. To determine the zeros of a polynomial function set the equation equal to zero.
Example Find the zeros of
f(x) = x2 + 4x + 3.
Step 1. Set the equation equal to zero.
x 2 + 4x + 3 = 0
Step 2. Solve for x, in this case by factoring.
(x + 3)(x + 1) = 0
Step 2a. Set each binomial equal to zero.
x + 3 = 0 or x + 1 = 0
Step 2b. Find the values of x.
x = -3 or x = -1
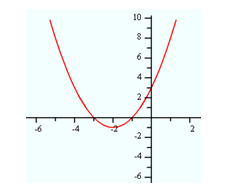
*Note: the y-intercept is 3, found when x = 0 ? f(0) = 02 + 4?0 + 3 = 3.
Complex Roots
The graph of a polynomial can intersect the x-axis at a maximum of n points, where n is the degree of the polynomial. A real polynomial can have real and/or imaginary roots. To explore complex roots of polynomial functions, please visit the SOS Math website topic entitled "Factoring over the Complex Numbers:"
Generalizations
Some useful deductions about roots of a polynomial equation and their nature are:
- A polynomial equation of order n can have a maximum of n roots, real or imaginary.
- Imaginary roots occur in pairs like 1+3i and 1-3i.
- Roots having square root terms occur in pairs like 1+?3 and 1-?3.
- If a polynomial equation involves only even powers of x and all terms are positive, then all roots of polynomial equation are imaginary (complex). For example, roots of the quadratic equation x4 + 2x2 + 4 = 0 are complex.
Descartes Rules of Signs
Descartes Rules of Signs is used to determine the number of positive and/or negative real roots of a polynomial function. The rules are:
- Maximum number of positive real roots of a polynomial equation f(x) is equal to the number of sign changes in f(x).
- Maximum number of negative real roots of a polynomial equation f(x) is equal to the number of sign changes in f(-x).
Example Determine the number of real roots of
f (x) = x3 + 3x2 ? 12x + 3 = 0
- Notice the signs are +, +, -, +. There are two sign changes as we move from left to right. Therefore, this cubic polynomial can have at most two positive real roots.
- To find f(?x), replace every x with negative x.
f(-x) = (?x)3+ 3(-x)2 -12(-x) + 3 = 0
f(-x) = ?x3+ 3x2 +12x + 3 = 0
-
Notice the signs are -, +, +, +. There is one sign change as we move from left to right. Therefore, the polynomial equation can have at most one negative root.
Sources
Sources used in this book:Embracing Mathematics, Assessment & Technology in High Schools; a Michigan Mathematics & Science Partnership Grant Project
Holt, Rinehart, and Winston, "Polynomial Functions." http://my.hrw.com/math06_07/nsmedia/homework_help/alg2/alg2_ch06_07_homeworkhelp.html (accessed 6/16/2010
S. O. S. Math, "Factoring Over Complex Numbers." 2010.http://www.sosmath.com/algebra/factor/fac09/fac09.html (accessed 6/16/2010).
Stapel, Elizabeth. "Descartes' Rule of Signs." Purplemath. Available from http://www.purplemath.com/modules/drofsign.htm. Accessed 16 June 2010.
Sunil Singh, "Polynomial function," Connexions, August 5, 2008, http://cnx.org/content/m15241/1.13/.