Graphical Behavior
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra II KHauck |
| Book: | Graphical Behavior |
| Printed by: | Guest user |
| Date: | Monday, January 5, 2026, 3:31 AM |
Description
Zero Polynomial
The zero polynomial function is defined as: y = f(x) = 0.
The graph of the zero polynomial is the x-axis. The domain of the zero polynomial is all Real numbers and the range is zero. Remember, the domain of a function is the set of values of the independent variable (x) for which the function is defined. The range of a function is the set of values of the dependent variable (y) for which the function is defined.
Constant Function
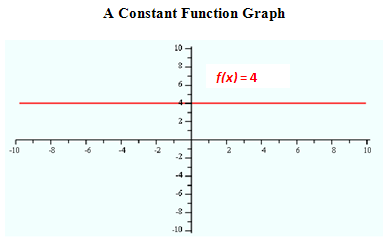
A constant function is a polynomial of degree 0. For example f(x) = 4; any value selected for x will always yield a value of 4 for the y-value. In general, when f(x) = c; any value selected for x will yield c for the y-value. The graph of a constant function will be a horizontal line intersecting the y-axis at the value of c. It is a line with slope equal to zero (m = 0).
Linear Function
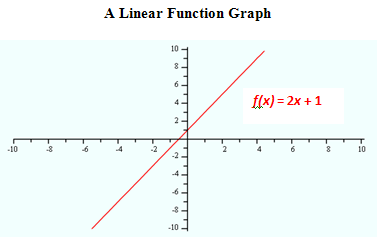
A linear function is a polynomial of degree 1, and the graph will be a line. In general, a linear function is f(x) = mx+ b; where m is the slope of the line and b is the y-intercept. The domain and range of linear functions is all Real numbers for both.
Quadratic Function
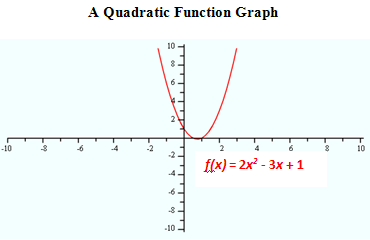
A quadratic function is a polynomial of degree 2, and the graph will be a parabola. In general, a quadratic function is
f(x) = ax2 + bx+ c; where a, b, and c, are real numbers and a does not equal zero. The domain of a quadratic function is all Real numbers and the range will be determined by each individual function.
Higher Degree Functions
To learn more about the behavior of higher degree polynomial functions, please visit the Purplemath website topic entitled, "Degrees, Turnings and Bumps:"
End Behavior
To explore end behavior of polynomial functions, please visit the Purplemath website topic entitled, "Polynomial Graphs: End Behavior:"
Video Lesson
Interactive Activity
This page contains an applet to help you explore polynomials of degree up to 5.
Guided Practice
To solidify your understanding of polynomial function end behavior, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.
Sources
Sources used in this book:Analyze Math, "Polynomial Functions." 11/8/2009.http://www.analyzemath.com/polynomial2/polynomial2.htm (accessed 12/7/2009).
Embracing Mathematics, Assessment & Technology in High Schools; a Michigan Mathematics & Science Partnership Grant Project
Holt, Rinehart, and Winston, "Polynomial Functions." http://my.hrw.com/math06_07/nsmedia/homework_help/alg2/alg2_ch06_07_homeworkhelp.html (accessed 6/4/2010).
Stapel, Elizabeth. "Degrees, Turnings, and 'Bumps'." Purplemath. Available from http://www.purplemath.com/modules/polyends4.htm. Accessed 16 June 2010
Sunil Singh, "Polynomial function," Connexions, August 5, 2008, http://cnx.org/content/m15241/1.13/.