Addition & Subtraction
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra II KHauck |
| Book: | Addition & Subtraction |
| Printed by: | Guest user |
| Date: | Monday, December 15, 2025, 11:34 PM |
Description
Adding Polynomials
To add polynomials, you must clear the parentheses, combine and add the like terms. In some cases you will need to remember the order of operations. Remember, when adding and subtracting like parts, the variable never changes.
Example 1 Add
(5x + 7y) + (2x - 1y)
Step 1. Clear the parentheses.
5x + 7y + 2x - 1y
Step 2. Combine like terms.
(5x + 2x) + (7y - 1y)
Step 3. Add like terms.
7x + 6y
Example 2 Add
(y2 - 3y + 6) + (y - 3y2 + y3)
Step 1. Clear the parentheses.
y 2 - 3y + 6+ y - 3y2 + y3
Step 2. Combine like terms.
y3 + (y2 - 3y2) + (- 3y + y) + 6
Step 3. Add like terms.
y 3 - 2y2 - 2y+ 6
Video Lesson
To learn how to add polynomial expressions select the following link to Holt, Rinehart and Winston:
Subtracting Polynomials
To subtract polynomials, you must change the sign of terms being subtracted using the Distributive Property. Clear the parentheses. Combine like terms.
Example 1 Subtract
(4x2 - 4) - (x2 + 4x - 4)
Step 1. Change the signs of the second polynomial expression.
(4x2 - 4) + (-x2 - 4x + 4)
Step 2. Clear the parentheses.
4x2 - 4 - x2 - 4x + 4
Step 3. Combine like terms.
(4x2 - x2) - 4x + (- 4 + 4 )
3x2 - 4x
Example 2 Subtract
(5x2 + 2x +1) - ( 3x2 – 4x – 2 )
Step 1. Change the signs of the second polynomial expression.
5x2 + 2x + 1 - 3x2 + 4x + 2
Step 2. Combine like terms.
(5x2 - 3x2) + (2x + 4x) + (1 + 2)
2x2 + 6x + 3
Video Lesson
To learn how to subtract polynomial expressions select the following link to Holt, Rinehart and Winston:
Subtracting Polynomial Expressions
Problem Solving
Using Addition or Subtraction of Polynomials
An application of polynomials is their use in finding areas of a geometric object. In the following examples, we will see how the addition or subtraction of polynomials might be useful in representing different areas.
Example 1 Write a polynomial to represent the area of the figure.
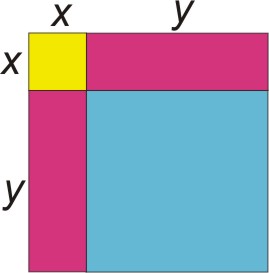
This shape is formed by two squares and two rectangles.
The blue square has area: y · y = y2. The yellow square has area: x · x = x2.
The pink rectangles each have area: x · y = xy.
To find the total area of the figure we add all the separate areas.
Total area = y2 + x2 + xy + xy = y2 + x2 + 2xy
Example 2
Write a polynomial to represent the area of the figure.
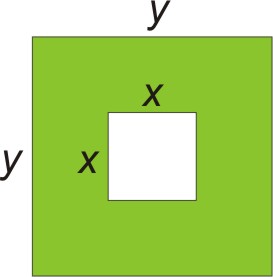
To find the area of the green region, we find the area of the big square and subtract the area of the little square.
The big square has area y · y = y2. The little square has area x · x = x2.
Area of the green region = y2 - x2.
Interactive Activity
Select the link below to test your knowledge with a practice quiz on adding and subtracting polynomials.
Guided Practice
To solidify your understanding of adding and subtracting polynomials, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.
Practice
Adding & Subtracting Polynomials Worksheet*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,†refresh your browser.
Answer Key
Adding & Subtracting Polynomials Answer Key
*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,†refresh your browser.
Sources
Sources used in this book:About Mathematics, "Adding and Subtracting Polynomials." 2010. http://math.about.com/library/blpoly.htm (accessed 12/3/2009).
Embracing Mathematics, Assessment & Technology in High Schools; a Michigan Mathematics & Science Partnership Grant Project
Holt Rinehart & Winston, "Exponents and Polynomials Homework Help Online." http://my.hrw.com/math06_07/nsmedia/homework_help/alg1/alg1_ch07_06_homeworkhelp.html (accessed 6/4/2010).
Hostos Community College, "Basic Operations of Polynomials." http://www.hostos.cuny.edu/oaa/compass/algebra_prac2.htm(accessed 12/4/2009).