Foundations

Site:	Clare-Gladwin RESD
Course:	Michigan Algebra II KHauck
Book:	Foundations

Printed by:	Guest user
Date:	Sunday, 19 May 2024, 7:05 PM

Description

Introduction
- Vocabulary
Degrees
- Multiple Variables
- Monomials
Standard Form
Combining Like Terms
- Video Lesson
Practice
- Answer Key
Sources

Introduction

The Algebra I course covered linear, quadratic, exponential & polynomial functions. In this section we will further explore polynomial functions. A polynomial is composed of multiple terms that contain positive integer exponents.

5x² - 2x is a polynomial.

3x² - 2x^-2is not a polynomial because it has a negative exponent.

$$ \sqrt{x-1} $$ is not a polynomial because it has a variable under the square root.

$$ \frac{5}{x^{3}+1^{}^{}} $$ is not a polynomial because it has an exponent in the denominator of a fraction.

$$4x^{0.3}$$ is not a polynomial because it has a decimal exponent.

Vocabulary

Terms of a polynomial are separated by addition. The example below is a polynomial with four terms.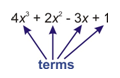

A variable is the unknown quantity represented by a letter, such as x in the example. A coefficient is the number in front of the variable in each term. If there is a subtraction sign, then the coefficient is negative. A constant is a number without a variable.

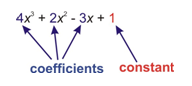
In this case, the coefficient of 4x³ is 4, the coefficient of 2x² is 2, the coefficient of -3x is -3, and the constant is 1.

Degrees

Each term in the polynomial has a degree. In single variable polynomials the degree is the value of the exponent. In the example:

4x³ + 2x² - 3x + 1

4x³ has a degree of 3 and is called a cubic term or 3^rd order term,

2x² has a degree of 2 and is called the quadratic term or 2^nd order term,

-3x has a degree of 1 and is called the linear term or 1^st order term,

1 has a degree of 0 and is called the constant.

The degree of a polynomial is the same as the degree of the term with the largest exponent. Since the largest exponent in our example is 3, the polynomial is of degree 3, also called a "cubic" polynomial.

Multiple Variables

Polynomials and terms can have more than one variable. Here is another example of a polynomial:

t⁴ - 6s³t² - 12st + 4s⁴ - 5

The positive integer exponents confirm this example is a polynomial. The polynomial has five terms. Let's look at each term more closely. When a term has multiple variables, the degree of the term is the sum of the exponents within the term.

t⁴ has a degree of 4, so it's a 4^th order term,

-6s³t² has a degree of 5 (3+2), so it's a 5^th order term,

-12st has a degree of 2 (1+1), so it's a 2^nd order term,

4s⁴ has a degree of 4, so it's a 4^th order term,

-5 is a constant, so its degree is 0.

Since the largest degree of a term in this polynomial is 5, then this is a polynomial of degree 5 or a 5^th order polynomial.

Monomials

A polynomial that has only one term is called a monomial (mono means one). A monomial can be a constant, a variable, or a product of a constant and one or more variables. You can see that each term in a polynomial is a monomial. A polynomial is the sum of monomials. Here are some examples of monomials:

5

-6x⁴y²z

2t

Standard Form

Each term in a polynomial has a degree. The term with the largest degree determines the degree of the polynomial. In order for a polynomial to be in standard form, the term with the largest degree must be listed first followed by the remaining terms in descending order of degree.

The following polynomials are in standard form:

4x⁴ - 3x³ + 2x² - x +1

a⁴b³ - 2a³b³ + 3a⁴b- 5ab² +2

The first term of a polynomial in standard form is called the leading term and the coefficient of the leading term is called the leading coefficient.

The first polynomial above has a leading term of 4x⁴ and a leading coefficient of 4.

The second polynomial above has a leading term of a⁴b³ and a leading coefficient of 1.

Combining Like Terms

A polynomial is in simplest form if all like terms have been combined. Like terms have the same variable(s) with the same exponents, but can have different coefficients.

2x²y and 5x²y are like terms

6x²y and 6xy² are not like terms

If a polynomial has like terms, we simplify it by combining (adding) them.

This sample polynomial is simplified by combining the like terms of 6xy and - 4xy giving us 2xy. We write the simplified polynomial as x² + 2xy + y².

Video Lesson

To learn how to combine like terms select the following link to Holt, Rinehart and Winston :

Combining Like Terms

Practice

Polynomial Foundation Worksheet

*Note: If Google Docs displays â€œSorry, we were unable to retrieve the document for viewing,â€ refresh your browser.

Answer Key

Polynomial Foundations Answer Key