Inverse Functions
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra II KHauck |
| Book: | Inverse Functions |
| Printed by: | Guest user |
| Date: | Friday, November 22, 2024, 1:39 AM |
Description
Introduction
An inverse function is a function that undoes another function, much like addition undoes subtraction. Inverse functions use inverse operations to turn inputs into outputs and vice versa.If a function answers the question: “How many hours of music fit on 12 CDs?†Then its inverse answers the question: “How many CDs do you need for 3 hours of music?â€
then the inverse function is modeled by 
. Since multiplication and division are inverse operations, they will create inverse functions.A common example of an inverse function is the Celsius-to-Fahrenheit conversion:
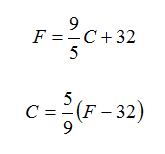
where C is the Celsius temperature and F the Fahrenheit temperature.
Notation
The function, f -1 (x) , is defined as the inverse function of f(x) if it consistently reverses the process of f(x). That is, if f(x) turns a into b, then f -1 (x) must turn b into a. f -1 (x) is not an exponent and is read “the inverse of function f.†It is meant to be an inverse function, not a reciprocal.Composition
Example 1
Are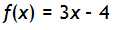 
and 
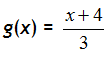inverses?
Step 1. Find the composition f (g(x))
Step 2. Find the composition g(f(x))
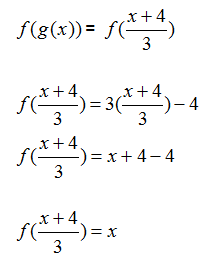
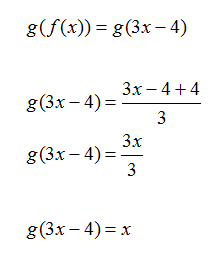
Step 3. Determine if the functions are inverses.
Since f(g(x)) = x and g(f(x)) = x, the functions are inverses.
Example 2
Are
and 
inverses? | Step 1. Find the composition f(g(x)) | Step 2. Find the composition g(f(x)) |
 |
 |
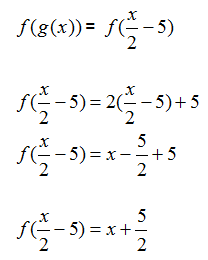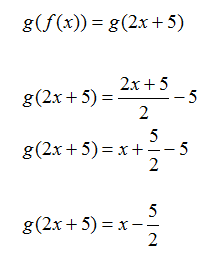Step 3. Determine if the functions are inverses.
Since
and
, the functions are NOT
inverses. To be inverses, both compositions must produce only x.
Inverse Function Graph
The graphs of inverse functions reflect over the line y = x. See the graph below:
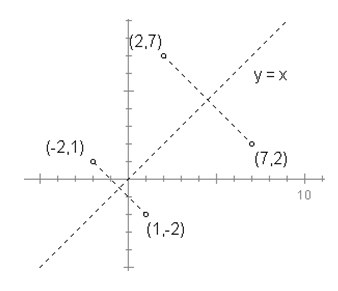
*Note: the reflection of the point (a,b) over the line y = x is the point (b,a) .
Example 1
Let f(x) = x3 + 2. Then f(2) = 10 and the point (2,10) is on the graph of f. The inverse of f must take 10 back to 2, i.e. f -1(10) = 2, so the point (10,2) is on the graph of f -1. The point (10,2) is the reflection over the line y = x of the point (2,10). The same argument can be made for all points on the graphs of f and f -1 . Therefore, the functions are inverses.
The graph of f -1 is the reflection over the line y = x of the graph of f.
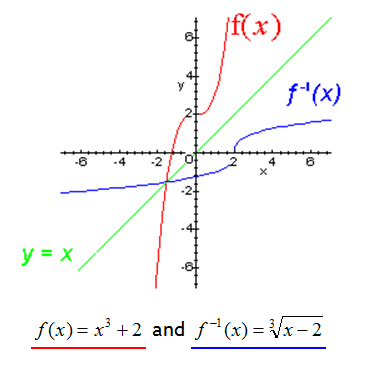
Example 2
If f has an inverse, then its graph will be the reflection of the graph of f over the line y = x. The graph of f and its reflection over y = x are drawn below.
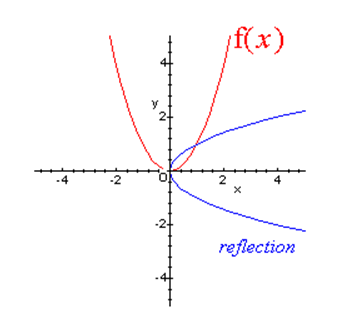
*Note: The reflected graph does not pass the vertical line test, so it is not the graph of a function.
Therefore, the function y = x2 does not have an inverse function.
The reflection of the graph is an inverse relation, but it is not a function.
Video Lesson
To learn how to graph inverse functions and relations, select the following link:
Finding Inverse Functions
Remember that an inverse function reverses the inputs and outputs. When we graph functions, we always represent the incoming number as x and the outgoing number as y. To find the inverse function switch the x and y values and then solve for y.
Example: Find the inverse function of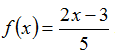 
.
Step 1. Replace f(x) with y in the equation describing the function.
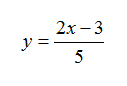
Step 2. Interchange x and y. In other words, replace every x with a y and vice versa.
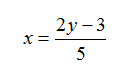
continued...
Example continued
Step 3. Solve for y.
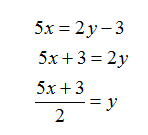
Step 4. Replace y with f-1(x).
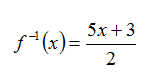
Step 5. Test to make sure this solution satisfies the definition of an inverse function.
Pick a number, and plug it into the original function: f(9) = 3
See if the inverse function reverses this process: f-1(3) = 9
Video Lessons
To learn how to write inverse functions, select the following link:
To learn how to write multi-step inverse functions, select the following link:
Practice
Familes of Functions Inverses Worksheet*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,†refresh your browser.
Answer Key
*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,†refresh your browser.
Sources
Sources used in this book:Embracing Mathematics, Assessment & Technology in High Schools; a Michigan Mathematics & Science Partnership Grant Project
Holt, Rinehart & Winston, . "Exponential and Logarithmic Functions." http://my.hrw.com/math06_07/nsmedia/homework_help/alg2/alg2_ch07_02_homeworkhelp.html (accessed 06/30/2010).
Kenny Felder, "Function Concepts -- Inverse Functions," Connexions, December 30, 2008, http://cnx.org/content/m18198/1.2/.
Ryson & Blond, " Graphs of a Function and the Inverse of the Function." http://www.members.shaw.ca/ron.blond/TLE/InvFcn.APPLET/index.html (accessed 06/30/2010).
UNC Wilmington, "Inverse Functions." http://www.uncwil.edu/courses/mat111hb/functions/inverse/inverse.html (accessed 6/29/2010).