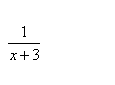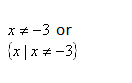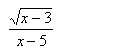Domain and Range
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra II KHauck |
| Book: | Domain and Range |
| Printed by: | Guest user |
| Date: | Sunday, 19 May 2024, 6:08 PM |
Description
Domain
The domain of a function is the set of values of the independent variable (x) for which the function is defined.There are two common mathematical operations that are undefined: square root of a negative number and division by zero.
Because a square root cannot successfully act on a negative number, the domain of
is all real numbers x such that 
. In set notation, this would be written 
.Division by zero is undefined; therefore values for x that produce a zero denominator are excluded from the domain. For instance, the function
has a domain of all real numbers except 
and 
. In set notation, this would be written 
.Examples
Function
|
Domain
|
Comments
|
|
|
If you substitute a value less than –7, it will result in a negative number under the radical sign. This operation would be undefined. |
|
|
|
Division by zero is undefined. |
|
|
|
If a value of x = -3 is substituted it produces a zero in the denominator, which is undefined. Be careful, the rule is not ,“When dividing, x cannot be 0.†The rule is “x can never be a value that would result in a zero denominator.†|
|
|
|
Any value can be substituted for x in this function and it will result in a number. |
|
|
 |
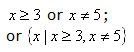Numbers less than 3 will result in a negative number under the radical sign and 5 causes a division by 0. |
Video Lesson
Range
The range of a function is the set of values of the dependent variable, y, for which the function is defined.
To illustrate range, consider the function 
. The domain of this function is all real numbers x such that 
; in other words, the input can be any number greater than or equal to –7.
What output does this function produce? Consider the following table of values:
Note as the x values increase, the y values also increase. However, the input 
is undefined. Hence, the range of this function is all real numbers y such that 
. In set notation, this would be written 
.
Interactive Activity
This demo is designed to help students use graphical representations of functions to determine the domain and the range.
Practice
Families of Functions Domain and Range WorksheetAnswer Key
Families of Functions Domain and Range Answer Key*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,†refresh your browser.
Sources
Sources used in this book:Embracing Mathematics, Assessment & Technology in High Schools; a Michigan Mathematics & Science Partnership Grant Project
Kenny Felder, "Function Concepts -- Domain and Range," Connexions, December 30, 2008, http://cnx.org/content/m18191/1.2/.
Roberts, Lila F.. "Domain and Range ." 09/12/2004.http://mathdemos.gcsu.edu/mathdemos/domainrange/domainrange.html (accessed 08/09/2010).