Transformations
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra II KHauck |
| Book: | Transformations |
| Printed by: | Guest user |
| Date: | Saturday, November 23, 2024, 1:42 AM |
Description
Transformation of Functions
Introduction
A transformation of a function shifts the parent function to another location on the coordinate plane. For this lesson we will focus on two types of transformations: translations and reflections. A translation shifts the graph left or right, or up or down. A reflection flips the graph across a line, such as the x or y-axis. For this lesson we will use the parent functions listed below:Linear: 
|
Power:  or 
|
Absolute Value: 
|
Square Root: 
|
Rational:  or 
|
Exponential: 
|
Logarithmic: 
|
Translation Up
When a constant is added to the outside of a function:
, the graph is translated up C units. Here is a graph of our parent function
and 
.
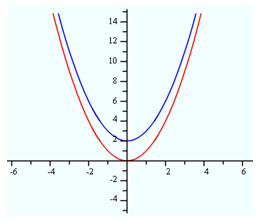
The translation of the parent graph is an upward shift of two.
Translation Down
When a constant is subtracted from the outside of a function:
, the graph is translated down C units. Here is a graph of our parent function
and 
.
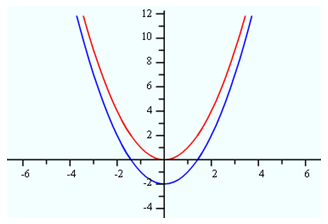
The translation of the parent graph is a downward shift of two.
Translation Left
When a constant is added to the inside of a function:
, the graph is translated left H units. Here is a graph of our parent function
and 
.
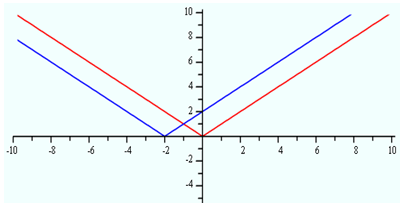
The translation of the parent graph is a shift of two to the left.
Translation Right
When a constant is subtracted from the inside of a function:
, the graph is translated right H units. Here is a graph of our parent function
and 
.
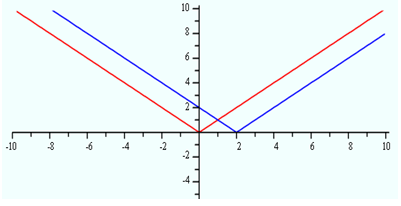
The translation of the parent graph is a shift of two to the right.
*Note: when adding or subtracting on the inside of the function, the shift is opposite the sign.
Reflection Across x-axis
When multiplying by a negative on the outside of a function:
, the graph reflects across the x-axis. Here is a graph of our parent function
and 
.
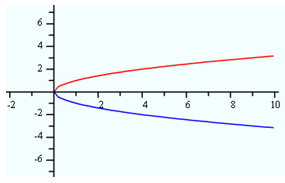
The translation of the parent graph is a reflection over the x-axis.
Reflection Across y-axis
When multiplying by a negative on the inside of a function:
, the graph reflects across the y-axis. Here is a graph of our parent function
and 
.
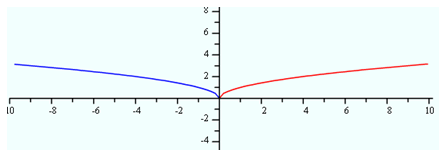
The translation of the parent graph is a reflection over the y-axis.
Rules to Remember
The transformations presented follow these rules:- f (x) + C is f(x) translated upward C units
- f (x) – C is f(x) translated downward C units
- f (x + H) is f(x) translated left H units
- f (x – H) is f(x) translated right H units
- –f(x) is f(x) reflected about the x-axis
- f (–x) is f(x) reflected about the y-axis
Combination of Transformations
Example 1
Graphs of the parent function 
and 
.
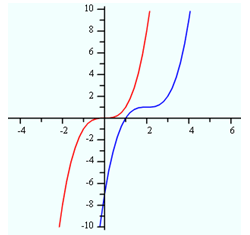
The parent function is translated upward one unit and two units to the right.
Example 2
and 
. 
The parent function is translated to the left three units and reflected over the x-axis.
Interactive Activity
This activity is designed to let the student work with families of functions.
Guided Practice
To solidify your understanding of transformations of functions, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials, and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.Transforming Functions Guided Practice
Practice
Transformations of Functions Worksheet*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,†refresh your browser.
 Video Lesson
Answer Key
Answers to Transformations of Functions Worksheet*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,†refresh your browser.
Sources
Sources used in this book:Embracing Mathematics, Assessment & Technology in High Schools; a Michigan Mathematics & Science Partnership Grant Project
Holt, Rinehart, & Winston, Polynomial Functions. "Rational and Radical Functions." http://my.hrw.com/math06_07/nsmedia/homework_help/alg2/alg2_ch06_08_homeworkhelp.html (accessed 06/30/2010).
May, Mike. "Families of Functions Applet." http://www.slu.edu/classes/maymk/Applets/FamilyGraphs.html (accessed 06/30/2010).