Exponential Growth
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra I |
| Book: | Exponential Growth |
| Printed by: | Guest user |
| Date: | Saturday, December 6, 2025, 4:36 PM |
Description
Exponential Growth
Growth & Decay
Exponential functions are functions where the base is a constant number and the exponent is a variable. The general exponential function takes the form: y = a · bx where a is the initial amount and b is the factor that the amount gets multiplied by each time x is increased by one.
There are two types of exponential functions, exponential growth and exponential decay. Exponential growth functions start out growing slowly and then grow faster and faster. There will be a consistent fixed period during which the function will increase by a fixed proportion. Exponential decay functions start out decreasing quickly and then decrease slower and slower. There is a consistent fixed period during which the function will decrease by a fixed proportion.
In this book, exponential growth functions will be discussed.
Growth Example 1
A colony of bacteria has a population of three thousand at noon on Sunday. During the next week, the colony's population doubles every day. What is the population of the bacteria colony at noon on Saturday?
Step 1. Determine the initial value.
Since the first day recorded is Sunday, the initial population is 3,000.
Step 2. Determine the growth factor.
Since the population is doubling, it is being multiplied by 2 each day. Therefore, the growth factor is 2.
Step 3. Write an exponential function.
The general form of an exponential function is ![]() .
.
This function is ![]() .
.
Step 4. Use the equation to solve the problem.
Since Saturday is 6 days after the initial day, Sunday, we will use x = 6.
![]()
Growth Example 2
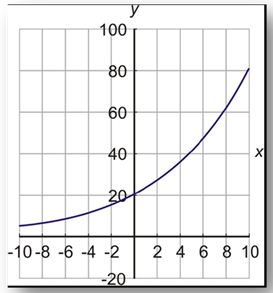
The population of a town is estimated to increase by 15% per year. The population today is 20,000. Make a graph of the population function and find out what the population will be ten years from now.
Step 1. Determine the initial value.
The initial population is 20,000.
Step 2. Determine the growth factor.
Since the population is increasing by 15% per year, it is being multiplied by 115% each day. Therefore, the growth factor is 1.15.
Step 3. Write an exponential function.
The general form of an exponential function is ![]() .
.
This function is ![]() .
.
Step 4. Use the equation to solve the problem.
Continued
Interactive Activity
For a visual understanding of exponential growth, select the following link:Exponential Growth Interactive
Video Lessons
To learn how to evaluate and solving exponential growth, select the following link:
Exponential Growth
Guided Practice
To solidify your understanding of exponential growth, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.Guided Practice
Practice
Exponential Growth WorksheetAnswer Key
Exponential Growth Answer KeySources
Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project
Gloag, Anne & Andrew. "Exponential Functions." February 24,
2010.http://www.ck12.org/flexr/chapter/4478
Holt, Rinehart, & Winston. "Exponential and Logarithmic Functions."
http://my.hrw.com/math06_07/nsmedia/homework_help/alg2/alg2_ch07_01_homeworkhelp.html (accessed September 9, 2010).
Mathwarehouse.com, "Exponential Growth in Real World ." http://www.mathwarehouse.com/exponential-growth/exponential-models-in-real-world.php (accessed 9/15/2010).