Tables
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra I |
| Book: | Tables |
| Printed by: | Guest user |
| Date: | Saturday, January 31, 2026, 4:11 PM |
Description
Tables
Exponential Functions
Exponential functions are written in the form: y = abx, where b is the constant ratio and a is the initial value. By examining a table of ordered pairs, notice that as x increases by a constant value, the value of y increases by a common ratio. This is characteristic of all exponential functions. In the table below notice that as the x-values increase by 1, the y-values double. In other words, to get from one y-value to the next, multiply by 2, therefore the common ratio is 2.
![]()
To find the equation that represents this table of values, substitute any ordered pair from the table into the equation, and solve for a.

So the model for this data is: ![]()
Example 1
Find an exponential model for the table below.
Step 1. Find the common ratio for the table.

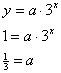
Step 3. Use the values of a and b to write an equation.
Example 2
Write an exponential model for the table below.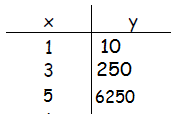
Step 1. Fill in the table to include the missing values for x.
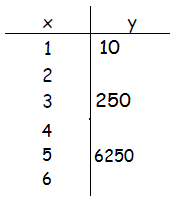
Example 2 Continued
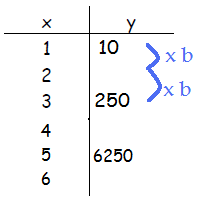
Since each value of y is moved 2 units for x, ![]() , or b2 is required to move between two points. To determine the b -value, set up an equation and solve.
, or b2 is required to move between two points. To determine the b -value, set up an equation and solve.
10•b2 = 250
b 2 = 25
b = 5
Step 3. Use an ordered pair to solve for the value of a.
For this example, use the point (1, 10)
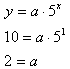
Step 4. Use the values of a and b to write an equation.
Video Lesson
To learn how to find models of exponential functions select the following link:Modeling Exponential Functions #1
Guided Practice
To solidify your understanding of writing exponential models, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.Guided Practice
Practice
Exponential Models WorksheetLight Intensity Worksheet
Answer Keys
Exponential Models Answer KeyLight Intensity Answer Key
Sources
Castellon, Carol. "Math 117 Lecture 9 notes."
http://www.math.uiuc.edu/~castelln/M117/lecture9_math117.pdf (accessed September 13, 2010).
Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project
Holt, Rinehart, & Winston. "Exonential and Logarithmic Functions."
http://my.hrw.com/math06_07/nsmedia/homework_help/alg2/alg2_ch07_08_homeworkhelp.html (accessed September 13, 2010).