Overview
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra I |
| Book: | Overview |
| Printed by: | Guest user |
| Date: | Saturday, January 31, 2026, 4:10 PM |
Description
Introduction
As discussed in the last book, another way to write a fractional exponent is with a radical sign. The examples below demonstrate how to translate a fractional exponent into a radical expression:
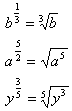
In cases where there are many terms under the radical sign it may be easier to simplify using roots rather than translating the expression to fractional exponents.
Square Roots
Taking the square root of a number is the inverse operation of squaring a number, just as adding is the inverse of subtracting. Therefore ![]() because
because ![]() and the operations cancel each other out. Remember from previous courses that 9 is a perfect square because it is the product of an integer with itself. Here is a list of the first twelve perfect square numbers.
and the operations cancel each other out. Remember from previous courses that 9 is a perfect square because it is the product of an integer with itself. Here is a list of the first twelve perfect square numbers.
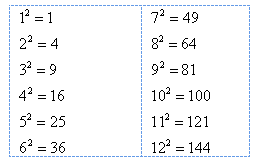
Memorizing the perfect square numbers will be beneficial when simplifying radical expressions.
It is also possible to take square roots of variables using the same process of looking for perfect squares. For example ![]() because the operations cancel each other out.
because the operations cancel each other out.
Cube Roots
Taking the cube root of a number is the inverse operation of cubing a number, just as adding is the inverse of subtracting. Therefore ![]() because
because ![]() and the operations cancel each other out. Remember from previous courses that 8 is a perfect cube because it is the product of three identical integers. Here is a list of the first six perfect cube numbers.
and the operations cancel each other out. Remember from previous courses that 8 is a perfect cube because it is the product of three identical integers. Here is a list of the first six perfect cube numbers.
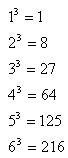
Memorizing the perfect cube numbers will be beneficial when simplifying radical expressions.
It is also possible to take cube roots of variables using the same process of looking for perfect cubes. For example ![]() because the operations cancel each other out.
because the operations cancel each other out.
Simplifying
Simplifying radicals is important when an exact value is required or to make a complex variable expression easier to manipulate. The first step is to determine what power is important by looking at the degree of the root. If the expression contains a cube root, then perfect cubes will be needed. Likewise, if the expression contains an nth root, then numbers or variables to the nth power will be needed. The Product Property of Roots is also needed and will be explained in greater detail later in this book.
Example 1 Simplify ![]() .
.
Step 1. Determine the degree of the root.
This expression is a square root, so the degree is 2.
Step 2. Find a perfect square factor under the radical.
![]()
Step 3. Use the Product Property of Roots to simplify.
![]()
Examples
Example 2 Simplify ![]() , assume all variables are positive.
, assume all variables are positive.
Step 1. Determine the degree of the root.
This expression is a cube root, so the degree is 3.
Step 2. Find perfect cube factors under the radical.
![]()
Step 3. Use the Product Property of Roots to simplify.
![]()
Example 3 Simplify ![]() , assume all variables are positive.
, assume all variables are positive.
Step 1. Determine the degree of the root.
This expression is a square root, so the degree is 2.
Step 2. Find perfect square factors under the radical.
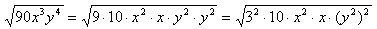
Step 3. Use the Product Property of Roots to simplify.
Video Lessons
To learn how to simplify radical expressions, select the following links to Khan Academy:
Simplifying Radical Expressions #1
Guided Practice
To solidify your understanding of simplifying radicals, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.Practice
Simplifying Radicals Worksheet
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Answer Key
Simplifying Radicals Answer Key
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Sources
Holt, Reinhart & Winston, "Exponential and Radical Functions ." http://my.hrw.com/math06_07/nsmedia/homework_help/alg1/alg1_ch11_06_homeworkhelp.html (accessed 1/8/2011).
Khan Academy, "Simplifying Radical Expressions 1." http://www.khanacademy.org/video/simplifying-radical-expressions1?playlist=Algebra%20I%20Worked%20Examples (accessed 1/8/2011).
Khan Academy, "Simplifying Radical Expressions 2." http://www.khanacademy.org/video/simplifying-radical-expressions-2?playlist=Algebra%20I%20Worked%20Examples (accessed 1/8/2011).
Khan Academy, "Simplifying Radical Expressions 3." http://www.khanacademy.org/video/simplifying-radical-expressions-3?playlist=Algebra%20I%20Worked%20Examples (accessed 1/8/2011).