Multipying & Dividing Rules
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra I |
| Book: | Multipying & Dividing Rules |
| Printed by: | Guest user |
| Date: | Sunday, December 21, 2025, 7:12 AM |
Description
Introduction
In previous courses, when working with the exponent on a number the instructions were to do the exponential operation. For example, 24 should be rewritten as 16, because it is the simplest form of ![]() . However with variables, exponents are used to simplify expressions, for example x7 is the simplified version of
. However with variables, exponents are used to simplify expressions, for example x7 is the simplified version of ![]() .
.
Example 1 Simplify ![]() .
.
This example is the multiplication of "y" 5 times, so it is simplified by writing: y5.
Example 2 Simplify (3a)(3a)(3a)(3a).
Step 1. Rearrange so that all numbers are grouped and all variables are grouped.
![]()
Step 2. Multiply the numbers.
![]()
Step 3. Use exponents to simplify the variables.
![]()
*Note: Remember that when taking powers of negative numbers, you must take into account how many times the sign is being multiplied. Even powers of negative numbers create a positive number and odd powers of negative numbers create a negative number.
Product of Powers
How does an expression like ![]() simplify? Notice that both terms have the same base. When a product of two or more terms has the same base to a power, the exponents can be added.
simplify? Notice that both terms have the same base. When a product of two or more terms has the same base to a power, the exponents can be added.
Product of Powers Rule: xn · xm = xn+m
Why does this rule work? Using the expression above and writing out the expansion of each term creates the following steps:
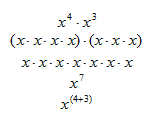
This rule is a nice "shortcut" for the multiplication of terms, but it only applies to exponents with the same base. Therefore, it will not work for ![]() , because the bases are not the same.
, because the bases are not the same.
Examples
Example 1 What is the product of z12 and z3?
Step 1. Verify the bases are the same.
Both terms have a base of z.
Step 2. Use the Product of a Power Rule to multiply the terms.
![]()
Example 2 What is the product of x2 and x4?
Step 1. Verify the bases are the same.
Both terms have a base of x.
Step 2. Use the Product of a Power Rule to multiply the terms.
![]()
More Examples
Example 3 What is the product of y2 and x4?
Step 1. Verify the bases are the same.
These terms do not have the same base, so the rule can not be used.
Therefore, the product is x4y2.
Example 4 What is the product of 23 and 24?
Step 1. Verify the bases are the same.
Both terms have a base of 2.
![]()
*Note: When using the product rule on numbers; do not multiply the bases until the very end of the process.
Video Lesson
To see a video lesson about the product of powers, select the following link:
Product Practice
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Answer Key
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Quotient of Powers
How does an expression like ![]() simplify? Notice that both terms have the same base. When there is a quotient of two terms with the same base to a power, the powers can be subtracted.
simplify? Notice that both terms have the same base. When there is a quotient of two terms with the same base to a power, the powers can be subtracted.
Quotient of a Power Rule: ![]()
Why does this rule work? Using the expression above and writing out the expansion of each term creates the following steps:
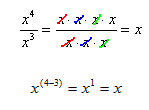
In other words, when dividing expressions with the same base keep the base and subtract the exponent in the denominator from the exponent in the numerator. This rule is a nice "shortcut" for the division of terms, but it only applies to exponents with the same base. Therefore, it will not work for ![]() , because the bases are not the same.
, because the bases are not the same.
Examples
Example 1 What is the quotient of x7 and x4?
Step 1. Verify the bases are the same.
Both terms have a base of x.
Step 2. Use the Quotient of a Power Rule to divide the terms.
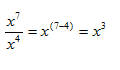
Example 2 Simplify ![]() .
.
Step 1. Verify the bases are the same.
These terms do not have the same base, so the rule can not be used.
Therefore, the simplest form is ![]() .
.
Example 3
Simplify ![]() .
.
Step 1. Verify the bases are the same.
Both terms have a base of a and b.
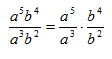
Step 3. Use the Quotient of a Power Rule on each base to divide the terms.
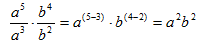
Example 4
What is the quotient of x3 and x8?
Step 1. Verify the bases are the same.
Both terms have a base of x.
Step 2. Use the Quotient of a Power Rule to divide the terms.
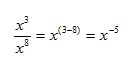
*Note: This answer contains a negative exponent. However, an algebraic expression is in simplest form when it is written with only positive exponents.
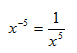
This answer can be verified by doing the division in expanded form: 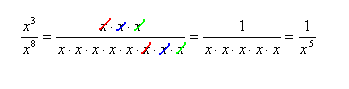
More details on negative exponents will be presented in the "Zeros and Negative Exponents" book later in this unit.
Video Lesson
To see a video lesson about the quotient of a power, select the following link:
Quotient Practice
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Answer Key
Quotient of a Power Answer Key
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Interactive Activity
Select the following link for more practice on the same base rules.
Guided Practice
To solidify your understanding of multiplying and dividing with exponents, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.
Sources
Gloag, Andrew & Anne. "Exponential Functions. "
http://www.ck12.org/flexr/chapter/4478 (accessed August 31, 2010)
Holt, Rinehart, & Winston. "Exponents and Roots."
http://my.hrw.com/math06_07/nsmedia/homework_help/msm3/msm3_ch04_03_homeworkhelp.html (accessed September 1, 2010)
Holt, Rinehart & Winston , "Lesson 2-7 Guided Practice Exercises." http://go.hrw.com/math/midma/gradecontent/loadlesson.html?course=c3&chapter=2&lesson=7&SE=1&sz_audio=1&calc=1&state=xx&actCourse=4 (accessed 9/8/2010).
Stapel, Elizabeth. "Negative Exponents." Purplemath. Available from http://www.purplemath.com/modules/exponent2.htm. Accessed 26 August 2010