Tables
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra I |
| Book: | Tables |
| Printed by: | Guest user |
| Date: | Monday, December 1, 2025, 7:40 AM |
Description
Tables
Introduction
In certain situations, the table of values for a polynomial function is known, but the equation is not. To model a polynomial function using a table, work the steps in finding the x-intercepts of a polynomial backwards. First, determine the zeros of the function by looking at the table. Second, turn each zero into a factor of the function. Finally, determine the factored form of the polynomial.Example 1 Determine the function that models the table below: 
Step 1. Determine the zeros of the function.
(-5, 0), (1, 0), (3, 0)
Step 2. Turn each zero into a factor of the function.
Since x = -5, then (x + 5) is a factor of the polynomial.
Since x = 1, then (x - 1) is a factor of the polynomial.
Since x = 3, then (x - 3) is a factor of the polynomial.
30 = a (0 + 5)(0 - 1)(0 - 3)
30 = a (15)
2 = a
Finding Differences
There is a method that can be used to determine the degree of a polynomial just by using a data table. This method is called finite differences. To find the exact equation for the polynomial function, you need to find the coefficients by solving a system of equations or using some other method. This will be covered in later mathematics classes.If you have a set of data with equally spaced x-values, you can find the lowest possible degree of a polynomial function that fits the data, if there is one, by analyzing the differences in the y-values. This technique, the finite differences method, determines only the degree of the polynomial. The steps are as follows:
Method of Finite Differences Algorithm
- List the terms as a sequence of numbers.
- Find the differences between successive terms until a constant is reached for every difference.
- Count the number of times it was necessary to subtract to get a common difference.
- The number of subtractions is the degree of the polynomial describing the sequence.
Example
The table below contains sets or ordered pairs from an unknown polynomial function. Use finite differences to determine the degree of the polynomial.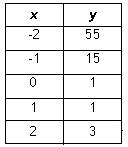
Step 1. Make sure the x-values are in equal increments.
The x-values of the table are increasing by one.
Step 2. Find the first difference of the table.
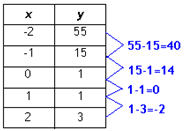
Example Continued
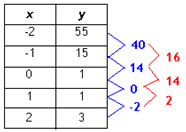
Since the second difference is not constant, the polynomial is not a quadratic.
Step 4. Find the third difference.
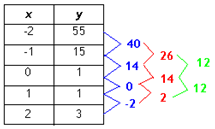
Since the third difference is constant, this table can be modeled by a third degree polynomial.
Video Lesson
For a video lesson on finding the degree of a polynomial, select the following link:Degree of Polynomials
Guided Practice
To solidify your understanding of writing a function from a graph & table, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.Guided Practice
Practice
Answer Keys
Sources
Boast, Steve. "Finding Differences Lab." 08/02/2000. webs.wichita.edu/facsme/cbl/algebra2/finitedif.pdf (accessed 08/12/2010).
Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project
Holt, Rinehart & Winston, "Polynomial Functions." http://my.hrw.com/math06_07/nsmedia/homework_help/alg2/alg2_ch06_09_homeworkhelp.html (accessed 9/8/2010).
Holt, Rinehart & Winston, "Using Finite Differences to Determine Degree." http://my.hrw.com/math06_07/nsmedia/lesson_videos/alg2/player.html?contentSrc=6459/6459.xml (accessed 9/8/2010).
Texas Instruments, "Count the Differences." http://education.ti.com/educationportal/activityexchange/Activity.do?cid=US&aId=12091 (accessed 08/12/2010).