Print bookPrint book

Factoring Special Patterns

Site: Clare-Gladwin RESD
Course: Michigan Algebra I
Book: Factoring Special Patterns
Printed by: Guest user
Date: Wednesday, January 15, 2025, 2:53 PM

Description

Factoring Special Patterns

Table of contents

Introduction

In the quadratic unit, there were patterns, that if recognized, made it easier to factor. They were the difference of squares and the perfect square trinomial. There are special patterns with other polynomials that will make it easier to factor them as well.


Sum & Difference of Cubes

If you have a cubic polynomial that is the sum or difference of two perfect cubes, the following special products can be used to factor the polynomial:

Sum of Cubes: x 3 + y3 = (x + y) (x2 - xy + y2)

Difference of Cubes: x 3 - y3 = (x - y) (x2 + xy + y2)

Example Factor the following polynomial: 64x3 + 125.

Step 1. Determine if you have a sum or difference of two cubes.

64x3 is (4x)3 and 125 is 53, so this is a sum of cubes.

Step 2. Use the pattern to factor.

(x + y) (x2 - xy + y2); x = 4x and y = 5

Sum&Difference1

*Note: Using Distributive Property to multiply the two terms will verify the polynomial was factored completely.

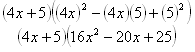
General Rules for Factoring

Use this checklist to help determine how to factor a polynomial:
  • Factor out the greatest common factor first, if possible.
  • If the polynomial to be factored is a binomial, then it may be a difference of two squares, or a sum or difference of two cubes (remember that a sum of two squares does not factor).
  • If the polynomial to be factored is a trinomial, then:
    • the polynomial may be a perfect square if two of the three terms are perfect squares.
    • the polynomial may be one of the general forms.
  • If the polynomial to be factored consists of four or more terms, try factoring by grouping.
  • Check if any of the factors can be factored further and do so when necessary.
  • Finally, check the factoring by multiplying the factors to determine if they equal the original polynomial.


Practice

Factor Special Patterns Worksheet
*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Answer Key

Factor Special Patterns Answer Key
*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Sources

Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project

Hensley, Patrica. "Genera; Advice for Factoring Polynomials." http://one.nettrekker.com/goExternal?np=/external.ftl&pp=/error.ftl&evlCode=35064&productName=school&HOMEPAGE=H (accessed 08/13/10).

Interactive Math, "Sum and Differences of Cubes." http://www.intmath.com/ FactFrac/4_SDCub.php (accessed 08/13/10).