Factor by Grouping
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra I |
| Book: | Factor by Grouping |
| Printed by: | Guest user |
| Date: | Saturday, December 6, 2025, 4:35 PM |
Description
Factor by Grouping
Introduction
Another way to solve polynomial equations is to factor. Similar to what was presented in the quadratics unit. There are multiple ways to factor polynomials. In a past unit, many trinomial quadratic equations were able to be factored. However, not all polynomials can be factored in this way. There might be more than three terms or the polynomial may not be made of perfect squares. When this happens, sometimes a common factor can be pulled out. Sometimes grouping the terms of the polynomial into two groups will help to factor the polynomial. Some of these ways will be discussed in this unit.If you need review of factoring trinomials, please select the following link:
Factoring Trinomials
Factoring
When a polynomial is written as the product of two or more polynomials, the polynomial has been factored. Here is an example:x 3 - 3x2 - 2x +6 = (x - 3)(x2 - 2)
The polynomials (x - 3) and (x2 - 2) are called factors of the polynomial. Note that the degrees of the factors, 1 and 2, respectively, add up to the degree of the original polynomial. Thus factoring breaks up a complicated polynomial into lower degree pieces. In this case, one of the factors can be factored further:
(x - 3)(x2 - 2) = (x - 3) (x + ![]() )(x -
)(x - ![]() )
)
Now that the polynomial has been factored into three linear or degree 1 polynomials, the polynomial cannot be factored any farther. Therefore, this polynomial has been factored completely.
Review of GCF
If a reminder is needed of factoring out the greatest common factor or GCF, please select the following links for a video lesson and guided practice:GCF Video Lesson
GCF Guided Practice
By Grouping
When polynomials have an even number of terms, sometimes they can be factored by grouping. The example below will demonstrate how to factor by grouping.Example Factor and solve the following polynomial:
![]()
Step 1. Use parentheses to group the terms into equal groups.
![]()
Step 2. Factor the GCF from each group.
![]()
Step 3. Since the two remaining factors are both (x + 3), use Distributive Property to regroup.
![]()
Step 4. Use Zero Product Property to solve the polynomial.
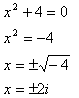 or
or ![]()
The Equal Test
It is possible to use a TI 83/84 calculator to check if the factoring is correct. In order to do this, follow these steps: Step 1. On the home screen, enter the original equation.
Step 2. Push the 2ND key and then the TEST key, then press #1 and ENTER to put an "=" sign in.
Step 3. Put in the factored form after the "=" and press ENTER.
Video Lessons
To learn more about factoring by grouping, please select the following links:Factor by Grouping #1
Factor by Grouping #2
Guided Practice
To solidify your understanding of factoring polynomials, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.Guided Practice #1
Guided Practice #2
Practice
Factor by Grouping WorksheetAnswer Key
Factor by Grouping Answer KeySources
Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project
Holt, Rinehart & Winston, "Factoring by Grouping." http://my.hrw.com/math06_07/nsmedia/lesson_videos/alg1/player.html?contentSrc=7550/7550.xml (accessed 9/8/2010).
Holt, Rinehart & Winston, "Factoring by Using the GCF." http://my.hrw.com/math06_07/nsmedia/lesson_videos/alg1/player.html?contentSrc=6366/6366.xml (accessed 9/8/2010).