Print bookPrint book

Inverses

Site: Clare-Gladwin RESD
Course: Michigan Algebra I
Book: Inverses
Printed by: Guest user
Date: Wednesday, January 15, 2025, 4:00 PM

Description

Inverses

Table of contents

Introduction

An inverse function is a function that undoes another function, much like addition undoes subtraction. Inverse functions use inverse operations to turn inputs into outputs and vice versa.

  • If a function answers the question: "Alice worked this long; how much money has she made?" Then its inverse answers the question: "Alice made this much money; how long did she work?"
  • If a function answers the question: "How many hours of music fit on 12 CDs?" Then its inverse answers the question: "How many CDs do you need for 3 hours of music?"

If a function is modeled by the rule, Inverses1, then the inverse function is modeled by Inverses2 . Since multiplication and division are inverse operations, they will create inverse functions.

The function, f -1(x), is defined as the inverse function of f(x) if it consistently reverses the process of f(x). That is, if f(x) turns a into b, then f -1(x) must turn b into a. f -1(x) is not an exponent. It is meant to be an inverse function, not a reciprocal.

The inverse has all the same points as the original function, except that the x and y-coordinates have been reversed. If the point (3,2) is a point in the original function then the point (2,3) will be a point of the inverse function.

It is possible to find the inverse of a set of points, a table, a graph or an equation. The set of points and the table work the same way. All three methods for finding inverses of functions will be discussed here.


Set of Points

Whenever a function is given as a list of ordered pairs, simply switch the x and y-values to create an inverse.

 

Example Find the inverse of PointsEx1-1, and determine if the inverse is a function.

Step 1. Switch the x and y-coordinates.

PointsEx1-2

Step 2. Determine if the inverse is a function.

Since every input has exactly one output, the inverse is a function. This function is called "one-to-one" which means every x and y value is used only once.

Listen

Equation

If given an equation, switch the x-and y-values and solve the resulting equation for y.

Example Find the inverse of the equation: EquationEx1-1

Step 1. Substitute a y for the f(x).

EquationEx1-2

Step 2. Switch the x and y-variables.

EquationEx1-3

Step 3. Solve the equation for y.

EquationEx1-4

Step 4. Substitute f-1(x) for y.

EquationEx1-5

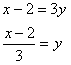
Linear Graph

The third method to find an inverse is by graphing. One of the characteristics of inverses is that they are symmetric about the line y = x also known as the identity line. When graphing inverses, switching the x and y-coordinates of a point and graphing on the other side of the line y = x will create an inverse.

Example Graph the inverse of the equation y = 2x + 3.

Step 1. Graph the equation y = 2x + 3.

Step 2. Graph the equation y = x.

Step 3. Find points on the line y = 2x + 3 and graph their symmetry points on the other side of the line y = x.

LinearGraph1

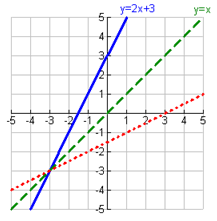
Remember, not all graphs produce an inverse that is also a function. This is true with quadratic graphs.


Quadratic Functions

A one-to-one function passes the horizontal line test as well as the vertical line test. In the graph of a function, no vertical line can pass through more than one point. In order to be a one-to-one function the same also has to be true for horizontal lines. No horizontal line can pass through more than one point of the graph.

The horizontal line test states: if any horizontal line intersects the graph of a function more than once, then the function does not have an inverse that is also a function.

Below are the graphs of y = x2 and x = y2:

InverseOf1

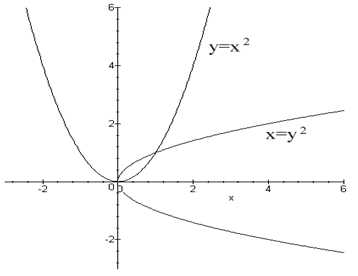
The graph of y = x 2 does not pass the horizontal line test so its inverse, x = y 2 is not a function. The graph of x = y 2 does not pass the vertical line test, so it verifies that the horizontal line test on the original function works. Therefore, the graph of f(x) = x 2 shows that Quadratic functions have inverse relations, but their inverses are not functions.


Video Lesson

To learn more about inverses, select the following link:

Inverses

Practice

Inverses Worksheet
*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Answer Key

Inverses Answer Key
*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Sources

Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project

Holt, Rinehart & Winston, "Inverse Functions." http://my.hrw.com/math06_07/nsmedia/lesson_videos/alg2/player.html?contentSrc=6481/6481.xml (accessed 8/22/2010).

"How to Find an Inverse Function." http://www.helpalgebra.com/articles/ inverseofafunction.htm (accessed 8/07/2010).

Regents Exam Prep Center, "Definition of Inverses." http://www.regentsprep.org/Regents/math/algtrig/ATP8/inverselesson.htm (accessed 08/07/2010).