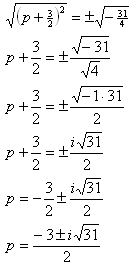Completing the Square
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra I |
| Book: | Completing the Square |
| Printed by: | Guest user |
| Date: | Monday, January 19, 2026, 2:57 AM |
Description
Completing the Square
Introduction
An equation in which one side is a perfect square trinomial can be easily solved by taking the square root of each side. Consider the example below.
When one side of the equation is not already a perfect square trinomial, the process taken to create a perfect square trinomial is called completing the square. Recall that a perfect square trinomial comes in one of two forms:
Steps
These steps should be followed to complete the square:|
Steps |
Example |
|
1. Be sure that the coefficient of the highest power is one. If it is not, divide each term by that value to create a leading coefficient of one. |
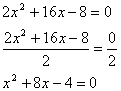
|
|
2. Move the constant term to the right hand side. |
|
|
3. Prepare to add the needed value to create the perfect square trinomial. Be sure to balance the equation. The boxes may help you remember to balance. |
|
|
4. To find the needed value for the perfect square trinomial, take half of the coefficient of the middle term (x-term), square it, and add that value to both sides of the equation. |
|
|
5. Factor the perfect square trinomial. |
|
|
6. Take the square root of each side and solve. Remember to consider both positive and negative results. |
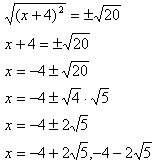
|
Example 1
Solve x2 + 6x + 1 = 0, by completing the square.Step 1. Be sure the leading coefficient is one.
Here the leading coefficient is one.
Step 2. Move the constant term to the other side of the equation.
![]()
Step 3. Find the correct c term to create a perfect square trinomial.
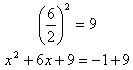
Step 4. Factor and simplify.
![]()
Step 5. Take the square root of both sides and simplify.
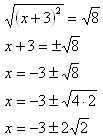
Example 2
Solve 2p2 + 20 = -6pStep 1. Be sure the leading coefficient is one.
The equation in standard form is: ![]() .The leading coefficient is 2.
.The leading coefficient is 2.
Divide all terms by 2 to get the equation: ![]()
Step 2. Move the constant term to the other side of the equation.
![]()
Step 3. Find the correct c term to create a perfect square trinomial.
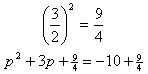
Step 4. Factor and simplify.
![]()
Step 5. Take the square root of both sides and simplify.
Video Lessons
To learn how to solve quadratics by completing the square, select one of the following links:Completing the Square #1
Completing the Square #2
Interactive Activity
To help understand why completing the square works, select the following link:Completing the Square
Guided Practice
To solidify your understanding of completing the square, visit the following links to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.Guided Practice #1
Guided Practice #2
Practice
Solve Quadratics by Completing the Square WorksheetAnswer Key
Solve Quadratics by Completing the Square Answer KeySources
Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project
Holt, Rinehart & Winston, "Quadratic Equations and Functions." http://my.hrw.com/math06_07/nsmedia/homework_help/alg1/alg1_ch09_08_homeworkhelp.html (accessed 7/24/2010).
Holt, Rinehart & Winston, "Quadratic Functions." http://my.hrw.com/math06_07/nsmedia/homework_help/alg2/alg2_ch05_04_homeworkhelp.html (accessed 7/24/2010).
The Biology Project, University of Arizona. "Quadratic Functions: Completing the Square." http://www.biology.arizona.edu/biomath/ tutorials/ Quadratic/CompletingtheSquare.html (accessed 7/13/2010).
NCTM, "Proof Without Words: Completing the Square." http://illuminations.nctm.org/ActivityDetail.aspx?ID=132 (accessed 07/24/2010).
"Quadratic Equations." http://www.jamesbrennan.org/algebra/quadratics/quadratic_ definitions.htm (accessed 07/15/2010).
Roberts, Donna. "Completing the Square." http://www.regentsprep.org/Regents/math/algtrig/ATE12/completesqlesson.htm (accessed 07/24/2010).