Solving Using Elimination
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra I |
| Book: | Solving Using Elimination |
| Printed by: | Guest user |
| Date: | Sunday, January 4, 2026, 10:20 PM |
Description
Elimination
Another method of symbolically solving a system of equations is elimination. When solving a linear system by elimination (sometimes called linear combination) simple addition and subtraction is used to simplify the system of equations to one equation involving a single variable. We begin with two unknowns (x and y) and move to a single unknown (either x or y), and, therefore, this method is often referred to as solving by elimination. One variable is eliminated in order to make the equations solvable. To accomplish this, something may need to be done to one, or both equations so that one variable will be eliminated.
Example 1
If one apple plus one banana costs $1.25 and one apple plus two bananas costs $2.00, how much does it cost for one banana? How much does it cost for one apple?
Step 1. Use a and b as the cost for apples and bananas, write two equations.
a + b = 1.25
a + 2b = 2.00
Step 2. Pretend the two equations create columns to add down and see if either variable will cancel.
![]()
Since neither variable will cancel automatically, move on to the next step.
Step 3. Determine which variable will cancel, then multiply one equation so that the variable will cancel.
In this equation the two "a" variables have the same coefficient and would cancel with opposite signs. Therefore, multiply one equation by -1.
a + b = 1.25
-1(a + b = 1.25)
-a - b = -1.25
Example 1 Continued
Step 4. Add down the "columns".
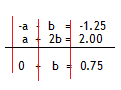
Step 5. Solve the remaining equation.
b = 0.75
Step 6. Substitute the variable from step 5 into either equation and solve for the remaining variable.
a + b = 1.25
a + 0.75 = 1.25
a = 0.50
Therefore, one apple will cost $0.50 and one banana will cost $0.75.
Example 2
Solve the system.
7x + 4y = 12
5x - 2y = 11
Step 1. Pretend the two equations create columns to add down and see if either variable will cancel.
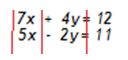
Since neither variable will cancel automatically, move on to the next step.
Step 2. Determine which variable will cancel, then multiply one equation so that the variable will cancel.
In this equation the 2 "y" variables have an easy GCF and would cancel if their coefficients were 4, -4. Therefore, multiply the second equation by 2.
2(5x - 2y = 11)
10x - 4y = 22
Step 3. Add down the "columns".
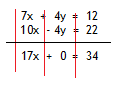
Example 2 Continued
Step 4. Solve the remaining equation.
17x = 34
x = 2
Step 5. Substitute the variable from step 4 into either equation and solve for the remaining variable.
7(2) + 4y =12
14 + 4y = 12
4y = -2
y = ![]()
The solution point is: x = 2 and y = ![]() .
.
Video lesson
To learn how to solve systems using elimination select the following link:
Guided Practice
To solidify your understanding of solving systems using elimination, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.
Practice
Systems by Eliminations Worksheet
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Answer Key
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Sources
Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project
Andrew and Anne Gloag, This chapter covers solving systems of equations graphically, Created: Jan. 18, 2010, http://www.ck12.org/flexr/search/Linear%20systmes%20of%20Equations/
Holt, Rinehart, & Winston. "Systems of Equations." http://my.hrw.com/math06_07/nsmedia/homework_help/alg1/
alg1_ch06_03_homeworkhelp.html (accessed August 4, 2010)