Parallel & Perpendicular Lines
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra I |
| Book: | Parallel & Perpendicular Lines |
| Printed by: | Guest user |
| Date: | Saturday, January 31, 2026, 4:11 PM |
Description
Parallel Lines
Parallel lines are lines that do not intersect. Parallel lines have the same slope; using this property, an equation of a line parallel to a given line can be written.
Example 1 Find the equation of the line parallel to y = 6x - 9 that passes through point (-1, 4)
Step 1. Find the slope of the given line.
y = 6x - 9 is written in slope-intercept form and has a slope = 6
Step 2. Use the point-slope form to write the equation.
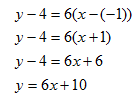
and parallel to the line y = 6x - 9
Example 2
Find the equation of the line parallel to 7 - 4y = 0 that passes through the point (9, 2).
Step 1. Rewrite the equation in slope-intercept form.
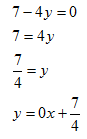
The slope of the given line is m = 0. This is a horizontal line.
Step 2. Substitute the values for m and the given point in the point-slope form and simplify.
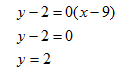
Example 3
Find the equation of the line parallel to 6x - 5y = 12 that passes through the point (-5, -3).
Step 1. Rewrite the equation in slope-intercept form.
![]()
The slope of the given line is ![]()
Step 2. Substitute the values for m and the given point into the point-slope form.
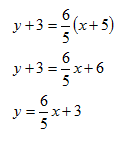
Perpendicular Lines
By definition, two lines are perpendicular if they intersect at right angles. Two lines with slopes m1 and m2 are perpendicular if ![]() . In other words the slopes of perpendicular lines are the opposite reciprocals of each other. For example, if the slope of a line is
. In other words the slopes of perpendicular lines are the opposite reciprocals of each other. For example, if the slope of a line is ![]() , then the slope of a line perpendicular to it is
, then the slope of a line perpendicular to it is ![]() . Using this property of the slopes of perpendicular lines, an equation of a line perpendicular to a given line can be written.
. Using this property of the slopes of perpendicular lines, an equation of a line perpendicular to a given line can be written.
Example 1
Find the equation of a line perpendicular to y = -3x + 5 that passes through the point (2, 6).
ÂStep 1. Find the slope of the given line y = -3x +5 .
m1 = -3
Step 2. Find the opposite reciprocal of the given slope.
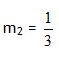
Step 3. Write an equation of a line with slope ![]() that passes through point (2, 6) using the point-slope form.
that passes through point (2, 6) using the point-slope form.
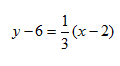
Step 4. Simplify.
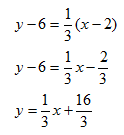
The equation of the line perpendicular is: ![]()
Example 2
Find the equation of the line perpendicular to x - 5y =15 that passes through the point (-2, 5).
Step 1. Rewrite the equation in slope-intercept form.
![]()
Step 2. Find the slope of the given line.
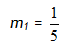
Step 3. Find the opposite reciprocal of the given slope.
m2 = -5
Step 4. Write an equation for a line with a slope m = -5 that passes through the point (-2, 5) using the point-slope form.
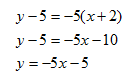
The equation of the perpendicular line is: ![]()
Example 3
Find the equation of the line perpendicular to y = -2 that passes through the point (4, -2).
The equation is already in slope intercept form but it has an x term of 0, making the equation y = 0x -2 . This means the slope is m = 0.
The negative reciprocal of 0 is ![]() The desired line will move 0 units in x for every 1 unit it rises in y. This is a vertical line, so the solution is the vertical line that passes through (4, -2). This is a line with an x coordinate of 4 at every point.
The desired line will move 0 units in x for every 1 unit it rises in y. This is a vertical line, so the solution is the vertical line that passes through (4, -2). This is a line with an x coordinate of 4 at every point.
The equation of the perpendicular line is: x = 4
Interactive
To practice writing equations for parallel and perpendicular lines, select the following link:
Parallel or Perpendicular?
Determining whether lines are parallel or perpendicular can be done by comparing the slopes of the lines. When given points on the line, find the slopes of each line using the slope formula. Then compare these slopes. When given the equations of the lines, rewrite each equation in slope-intercept form in order to find the slopes. Then compare these slopes.
Remember that parallel lines have the same slope, ![]() , but different y-intercepts. And perpendicular lines have slopes which are the opposite reciprocals of each other
, but different y-intercepts. And perpendicular lines have slopes which are the opposite reciprocals of each other ![]() . In otherwords, the product of the slopes of perpendicular lines equals -1 or
. In otherwords, the product of the slopes of perpendicular lines equals -1 or ![]() .
.
Example 1
Determine whether the lines are parallel, perpendicular or neither. One line passes through points (2, 11) and (-1, 2); another line passes through points (0, -4) and (-2, -10).
Step 1. Determine the slope of each line.
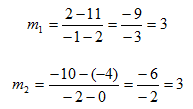
Step 2. Compare the slopes.
The slopes are equal, so the lines are parallel.
*Note: points from the same line would also produce equal slopes, verify that these are two different lines by graphing each set of points.
Example 2
Determine whether the lines are parallel, perpendicular or neither. One line passes through points (-2, -7) and (1, 5); another line passes through points (4, 1) and (-8, 4).
Step 1. Determine the slope of each line.
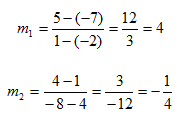
Step 2. Compare the slopes.
The slopes are opposite reciprocals of each other,
so the lines are perpendicular.
Example 3
Determine whether the lines are parallel, perpendicular or neither. One lines passes through points (3, 1) and (-2, -2); another line passes through points (5, 5) and (4, -6).
Step 1. Determine the slope of each line.
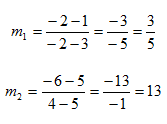
Step 2. Compare the slopes.
The slopes are not the same or opposite reciprocals of each other,
so the lines are neither parallel nor perpendicular.
Example 4
Determine whether the following lines are parallel, perpendicular or neither. Line 1: 3x + 4y = 2 Line 2 : 3x - 6y = 5
Step 1. Rewrite the equations in slope-intercept form and determine the slope of each.

Step 2. Compare the slopes.
The slopes are not the same or opposite reciprocals of each other,
so the lines are neither parallel nor perpendicular.
Example 5
Determine whether the lines are parallel, perpendicular or neither. Line 1: ![]() Line 2 :
Line 2 : ![]()
Step 1. Rewrite the equations in slope-intercept form and determine the slope of each.

The slopes are opposite reciprocals of each other,
so the lines are perpendicular to each other.
Example 6
Determine whether the lines are parallel, perpendicular or neither. Line 1: 7y + 1 = 7x Line 2: x + 5 = y .
Step 1. Rewrite the equations in slope-intercept form and determine the slope of each.

Step 2. Compare the slopes.
The slopes are the same and the intercepts are different, so the lines are parallel.
Video Lesson
To learn more about parallel and perpendicular lines, select the following link:
Guided Practice
To solidify your understanding of parallel and perpendicular lines, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.
Practice
Parallel and Perpendicular Lines Worksheet
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Answer Key
Parallel and Perpendicular Lines Key
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Sources
Gloag, Anne and Andrew "Writing Linear Equations", CK-12 Foundation's Algebra FlexBook, December 9, 2009, http://www.ck12.org/flexr/flexbook/738/
Holt, Rinehart, & Winston. "Linear Functions." http://my.hrw.com/
math06_07/nsmedia/homework_help/alg1/alg1_ch05_08_
homeworkhelp.html (accessed August 14, 2010).