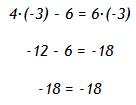Solving for a Variable
| Site: | Clare-Gladwin RESD |
| Course: | Michigan Algebra I |
| Book: | Solving for a Variable |
| Printed by: | Guest user |
| Date: | Monday, December 22, 2025, 3:40 AM |
Description
Addition & Subtraction
The process of solving one-step equations involving addition or subtraction, such as x + 6 = 3, is vital to understanding how to work with linear equations. To review how to solve for a variable, select the following link:
Review Solving One-Step Equations with Addition or Subtraction
Guided Practice
To solidify your understanding of solving one-step equations, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.
Multiplication & Division
The process of solving one-step equations involving multiplication or division, such as 2x = 5, is a necessary skill in solving linear equations. To review how to solve for a variable, select the following link:
Review Solving Equations Using Multiplication or Division
Example 1
Solve 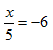
Step 1. Since the x is divided by 5, multiply both sides by 5.
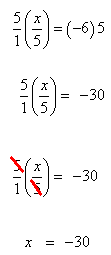
Step 2. Check the solution by substituting into the original equation.
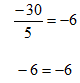
Example 2
Solve 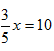 .
.
Step 1. Since x is multiplied by ![]() , divide both sides by
, divide both sides by ![]() which is the same as multiplying both sides by its reciprocal of
which is the same as multiplying both sides by its reciprocal of ![]() .
.
![]()
Step 2. Simplify.
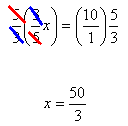
Step 3. Check the solution by substituting into the original equation.
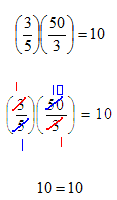
Guided Practice
To solidify your understanding of solving equations using multiplication and division, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.
Multi-Step Equations
In multi-step equations, the same techniques used in solving one-step equations will be used. Just like solving one-step equations, the goal is to have the variable with a coefficient of one on one side of the equal sign and a number on the other. Keep in mind that the variable does not always have to be x. Equations can make use of any letter as a variable.
The strategy for getting the variable by itself with a coefficient of 1 involves using opposite operations. Many linear equations require more than one step for their solution.
Example 3
Solve 7x + 2 = -54
Step 1. Subtract 2 from both sides of the equation to isolate the variable.
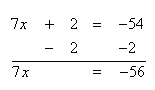
Step 2. Divide both sides of the resulting equation by the coefficient of 7 and simplify.
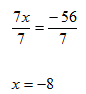
Step 3. Check the solution.
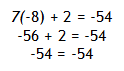
*Hint: When solving a multi-step equation follow the Order of Operations in
reverse order or SADMEP.
Example 4
Solve -5x - 7 = 108
Step 1. Add 7 to both sides of the equation to isolate the variable.
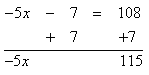
Step 2. Divide both sides of the resulting equation by -5 and simplify.
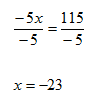
Step 3. Check the solution.
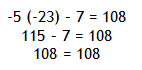
Example 5
Solve 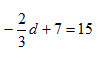
Step 1. Subtract 7 from both sides of the equation to isolate the variable.
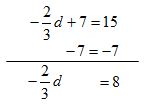
Step 2. Divide both sides of the resulting equation by ![]() and simplify. *Remember: multiplying both sides by the reciprocal of the coefficient yields the same result as dividing by the coefficient. Choose the easiest method.
and simplify. *Remember: multiplying both sides by the reciprocal of the coefficient yields the same result as dividing by the coefficient. Choose the easiest method.
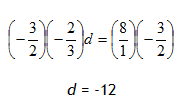
Step 3. Check the solution.
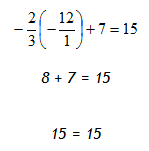
Combining Variables
In solving equations in the form ax + c = bx + d the goal remains to rewrite the equation in the form variable = constant. Begin by combining like terms so there is only one variable term and one constant term.
Example 6 Solve 5x + 7x = 72
Step 1. Combine like terms.
5x + 7x = 72
12x = 72
Step 2. Divide both sides of the resulting equation by 12 and simplify.
12x = 72
12 12
x = 6
Step 3. Check the solution.
5?6 + 7?6 = 72
30 + 42 = 72
72 = 72
Example 7
Solve 4x - 6 = 6x
Step 1. Use inverse functions to move like terms to the same side of the equation. Subtract 4x from both sides and simplify.
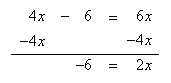
Step 2. Divide both sides of the resulting equation by 2 and simplify.
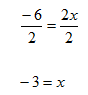
Step 3. Check the solution.
Example 8
Solve 8x - 1 = 23 - 4x
Step 1. Use inverse functions to move like terms to the same side of the equation. Add 4x to both sides and simplify.
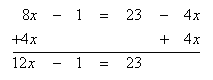
Step 2. Add 1 to both sides of the resulting equation and simplify.
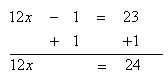
Step 3. Divide both sides of the resulting equation by 12 and simplify.
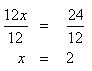
Step 4. Check the solution.
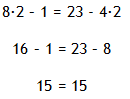
Example 9
Solve 5 + 4x - 7 = 4x - 2 - x
Step 1. Combine like terms that are on the same side of the equation.
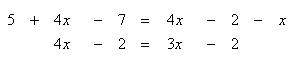
Step 2. Use inverse functions to move like terms to the same side of the equation. Subtract 3x from the resulting equation.
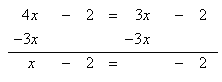
Step 3. Add 2 to both sides of the resulting equation.
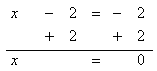
Step 4. Check the solution.
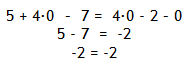
Special Cases
There are two special cases that may arise when solving equations. They occur when the variable is eliminated from the equation, leaving a constant on both sides. If the resulting statement is true, such as 2 = 2, then any real number can be substituted for the variable and a true statement will be created. Therefore, the solution is all real numbers.
The other case occurs when the statement is false, such as 6 = 7, then any real number substituted in for the variable will create a false conclusion. Therefore, there is no solution.
Example 10
Solve 11 + 3x - 7 = 6x + 5 - 3x
Step 1. Combine like terms that are on the same side of the equation.
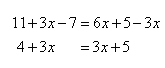
Step 2. From the resulting equation, subtract 3x from both sides.
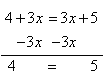
Since 4 = 5 is a false statement, there is no solution.
Example 11
Solve 6x + 5 - 2x = 4 + 4x + 1
Step 1. Combine like terms that are on the same side of the equation.
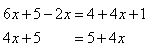
Step 2. From the resulting equation, subtract 4x from both sides.
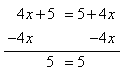
Since 5 = 5 is a true statement, all real numbers are solutions.
Distribution Property
When an equation contains parentheses, one of the steps in solving the equation requires the use of the Distributive Property. The Distributive Property is used to remove the parentheses from a variable expression by multiplying every term within the parentheses by the value in front of the parentheses.
Example 12
Solve 9 = 3(5x - 2)
Step 1. Use the Distributive Property to remove the parentheses.
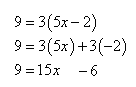
Step 2. Combine like terms in the resulting equation. Add 6 to both sides of the equation.
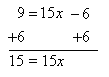
Step 3. Solve for x. Divide both sides of the resulting equation by 15 and simplify.
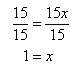
Step 4. Check the solution.
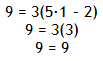
Example 14
Solve 7(5x - 2) = 6(6x - 1)
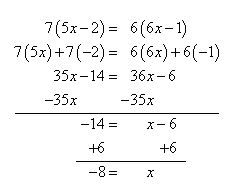
Solution Check
7(5? (-8) - 2) = 6(6?(-8) - 1)
7(-42) = 6(-49)
-294 = -294
Example 15
Solve 13 - (2x + 2) = 2(x + 2) + 3x
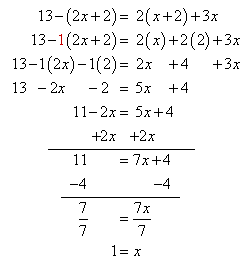
Solution Check
13 - (2?1+2) = 2(1+2) + 3?1
13 - 4 = 6 + 3
9 = 9
Video Lesson
To learn how to solve for a variable, select the following link:
Guided Practice
To solidify your understanding of solving for variables, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.
Practice
Solving Linear Equations Worksheet
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing,." refresh your browser
Answer Key
Solving Linear Equations Answer KeySources
Holt, Rinehart, & Winston. "Algebraic Reasoning. "http://my.hrw.com/math06_07/nsmedia/homework_help/msm3/msm3_ch01_11_homeworkhelp.html (accessed August 15, 2010)
Holt, Rinehart, & Winston. "Algebraic Reasoning. "http://my.hrw.com/math06_07/nsmedia/homework_help/msm3/msm3_ch01_08_homeworkhelp.html (accessed August 15, 2010)
Holt, Rinehart, & Winston. "Algebraic Reasoning."
http://my.hrw.com/math06_07/nsmedia/homework_help/msm3/msm3_ch11_03_homeworkhelp.html (accessed August 15, 2010)
Mainland High School, Algebra Lab. "Solving Multi-Step Equations." http://www.algebralab.org/lessons/lesson.aspx?file=algebra_onevariablemultistep.xml (accessed 08/21/2010).
Stapel, Elizabeth. "Solving Multi-Step Linear Equations." Purplemath. Available from http://www.purplemath.com/modules/solvelin3.htm . Accessed 15 August 2010