Factoring Special Patterns
Sum & Difference of Cubes
If you have a cubic polynomial that is the sum or difference of two perfect cubes, the following special products can be used to factor the polynomial:
Sum of Cubes: x 3 + y3 = (x + y) (x2 - xy + y2)
Difference of Cubes: x 3 - y3 = (x - y) (x2 + xy + y2)
Example Factor the following polynomial: 64x3 + 125.
Step 1. Determine if you have a sum or difference of two cubes.
64x3 is (4x)3 and 125 is 53, so this is a sum of cubes.
Step 2. Use the pattern to factor.
(x + y) (x2 - xy + y2); x = 4x and y = 5
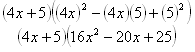
*Note: Using Distributive Property to multiply the two terms will verify the polynomial was factored completely.