Domain & Range
Example 2
The functionStep 1. Determine the domain.
Since this function is modeling a situation, the label of the inputs is important. In this situation, the input values are based on time and therefore, the domain is ![]() or the domain is all input greater than or equal to 0, since you cannot have negative time.
or the domain is all input greater than or equal to 0, since you cannot have negative time.
Step 2. Find the vertex.
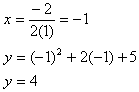
Step 3. Determine the range.
Since the graph opens down and the vertex is (-1, 4), the range should be ![]() . However, since -1 is not part of the input, the range will have to start at the first domain of 0. The range of the situation is
. However, since -1 is not part of the input, the range will have to start at the first domain of 0. The range of the situation is ![]() .
.