Ellipses
Example 4
Graph the following equation.
16x2 + 25y2 + 32x - 150y = 159
Step 1 . Identify the conic section.
This is an ellipse because the x and y terms are both squared,
have different coefficients, and are added.
Step 2 . Write equation in standard form.
(16x2+32x) + (25y2-150y) = 159; Group the x terms, group the y terms
16(x2+2x) + 25(y2-6y) = 159; Factor the leading coefficient from each group
16(x2+2x+1) + 25(y2-6y+9) = 159 + (16?1) + (25?9); Complete the square for x and y
16(x+1)2 + 25(y-3)2 = 400; Simplify
; Divide each side of the equation by 400 and simplify.
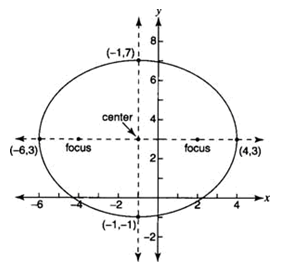
Step 3. Graph the conic.
Identify the center (-1, 3)
Identify the vertices (4, 3), (-6, 3)
Identify the co-vertices (-1, 7), (-1, -1)
